Question

A pyramid is cut by a plane parallel to its base at a distance from the base equal to the two-thirds of the length of the altitude. The area of the base is 18 square units. Find the area of the section determined by the pyramid and the cutting plane.
[a] 1
[b] 2
[c] 3
[d] 6
[e] 9

Answer 1

Hint: Use the fact that the ratio of areas of two similar figures is equal to the square of their corresponding side lengths. Assume that the length of a side of the base is equal to x. Find the length of the corresponding side of the section of the pyramid. Hence determine the ratio of the sides and hence determine the ratio of the areas and hence the area of the section.

Complete step-by-step answer:
Let the distance of the centre of the base from a vertex be x.

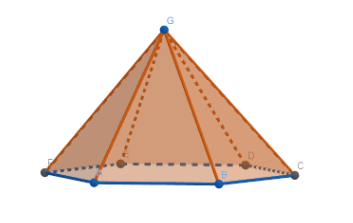
Consider the section of the pyramid as shown

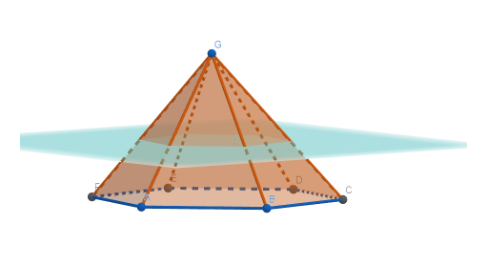
Visualising the section due to the plane in the above diagram

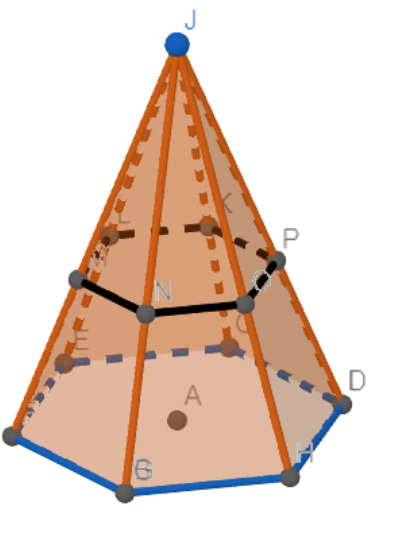
As is clear the section is also a polygon similar to the base of the pyramid.
Join the top of the pyramid with the centre of the base and the centre of the base with the vertex and the centre of the section with the corresponding vertex in the section.
This will form a triangle as shown below

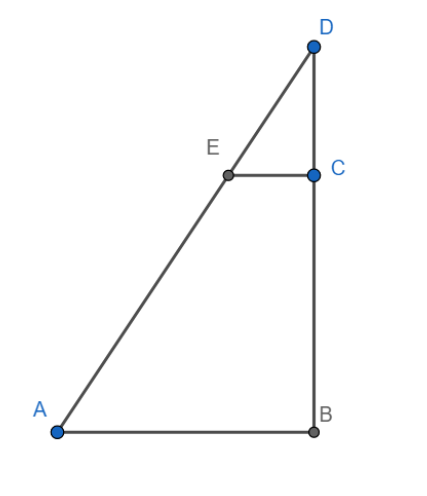
Here D is the top of the pyramid, C the centre of the section, B the centre of the base, A the vertex of base and E the corresponding vertex of the section.
Since the plane cuts at two-thirds the length of the altitude from the base, we have $\dfrac{DC}{DB}=\dfrac{1}{3}$
Now, in triangle ABD, we have EC||AB.
Hence, we have $\angle DEC=\angle DAB$ and $\angle DCE=DBA$
Hence, we have $\Delta DEC\sim \Delta DAB$(By AA similarity criterion)
Hence, we have
$\dfrac{EC}{AB}=\dfrac{DC}{DB}=\dfrac{1}{3}$
Since EC is a length in the section and AB the corresponding length in base polygon
Hence, we have
$\dfrac{ar\left( \text{section} \right)}{ar\left( \text{base} \right)}={{\left( \dfrac{1}{3} \right)}^{2}}$
Given the area of the base = 18
Hence, we have
$ar\left( \text{section} \right)=\dfrac{18}{9}=2$
Hence option [b] is correct.

Note: [1] The above question uses the property that the ratio of areas of two similar figures is equal to the squares of the ratio of the corresponding lengths in the figures. This is a consequence of the fact that the area is obtained as a product of lengths in the figure and since the lengths are proportional, the ratio of areas is the square of the ratio of corresponding lengths in the figures.