Question

A ray of light falls on a transparent glass slab of refractive index 1.62. If the reflected ray and refracted ray are mutually perpendicular, then the angle of incidence is:
(A) \[{58^ \circ }{15^{'}}\]
(B) \[{57^ \circ }{19^{'}}\]
(C) \[{58^ \circ }{19^{'}}\]
(D) \[{57^ \circ }{12^{'}}\]

Answer 1

Hint: In order to answer this question, we need to understand that by basic geometry, we know that the refracted angle should be 30° for the reflected and refracted ray to be perpendicular to each other. Now, we could substitute these values into Snell’s law of refraction (assuming the other medium is air) to get the refractive index of glass.
Formula Used:
Law of reflection,
Angle of incidence = angle of reflection
Snell’s Law,
\[\dfrac{{\sin \left( i \right)}}{{\sin \left( r \right)}}\]
Complete step-by-step solution:
Angle of reflection is the angle made by the reflected ray with the normal.
When a light ray is incident on a glass surface, there is a change in medium. So, the incident ray is getting refracted at the glass surface.
We are given the question that the reflected ray and the refracted ray lie perpendicular to each other.

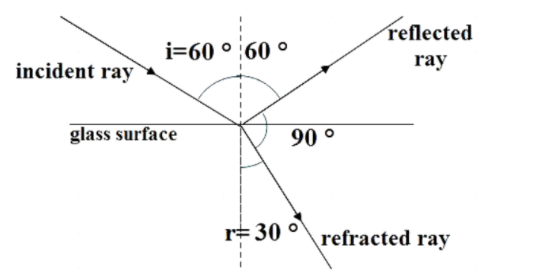
From the above diagram we can write it as,
\[i + r + {90^ \circ } = {180^ \circ }\]
Arranging it we get,
\[i + r = {180^ \circ } - {90^ \circ }\]
\[i + r = {90^ \circ }\]
\[r = {90^ \circ } - i\]
By law of reflection, we have that,
Angle of incidence (i) = angle of reflection
Now, let us recall Snell’s law which states that, ratio of the sine of the angle of incidence to that of refraction is a constant for a given pair of media. This constant is what we call the refractive index of that medium with respect to the refractive index of the medium in which light was incident. That is,
\[\mu = \dfrac{{\sin \left( i \right)}}{{\sin \left( r \right)}}\]
Substituting the value of \[r\] we get,
\[ \Rightarrow \mu = \dfrac{{\sin \left( i \right)}}{{\sin \left( {{{90}^ \circ } - i} \right)}}\]
We know that,
\[\sin \left( {90 - i} \right) = \cos \left( i \right)\]
\[ \Rightarrow \mu = \dfrac{{\sin \left( i \right)}}{{\cos \left( i \right)}}\]
We know,
\[\dfrac{{\sin \left( i \right)}}{{\cos \left( i \right)}} = tan\left( i \right)\]
\[ \Rightarrow \mu = \tan \left( i \right)\]
\[\therefore i = {\tan ^{ - 1}}\mu \]
It is given in question that,
\[\mu = 1.62\]
Substituting the value of \[\mu \] we get,
\[ \Rightarrow i = {\tan ^{ - 1}}\left( {1.62} \right)\]
\[ \Rightarrow {58^ \circ }{19^{'}}\]

Hence, the correct option is (D).

Note:
It should be remembered that while dealing with optics related problems, make sure that you draw a neat ray diagram prior to answering the question. By doing so you might be able to understand the problem more clearly and hence find the answer easily. Also, check whether the angle at which the ray strikes is given with respect to the glass surface or the normal.