
A rectangle has dimensions
Answer
430.5k+ views
Hint: We describe the relation between the sides of a rectangle and its area. We increase the length of the sides following the percentage increase. We find the change in areas and find its percentage.
Complete step by step solution:
It is given that the dimensions of the rectangle is
The area of the rectangle was
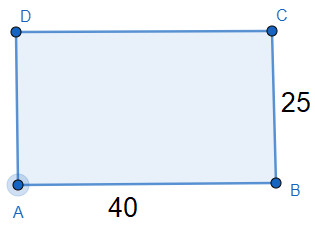
Now we have increased the length and breadth by 15%.
For the given percentage 15% of 40 and 15% of 25, we first need to find the mathematical form.
We know for any arbitrary percentage value of a%, we can write it as
Therefore, 15% increase on 25 can be written as
Therefore, 15% increase on 40 can be written as
The length and the breadth of the new rectangle becomes
The area of the new rectangle was
The increase in the area is
The percentage increase will be
Therefore, the percentage increase in the rectangle’s area is
Note: The value of the fraction is actually the unitary value of 15 out of 100. Therefore, in percentage value we got
Complete step by step solution:
It is given that the dimensions of the rectangle is
The area of the rectangle was

Now we have increased the length and breadth by 15%.
For the given percentage 15% of 40 and 15% of 25, we first need to find the mathematical form.
We know for any arbitrary percentage value of a%, we can write it as
Therefore, 15% increase on 25 can be written as
Therefore, 15% increase on 40 can be written as
The length and the breadth of the new rectangle becomes
The area of the new rectangle was
The increase in the area is
The percentage increase will be
Therefore, the percentage increase in the rectangle’s area is
Note: The value of the fraction is actually the unitary value of 15 out of 100. Therefore, in percentage value we got
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE





