
A rectangular field is 16 m long and 10 m wide. There is a path of uniform width all around it having an area of
Answer
428.7k+ views
Hint: Here in this question, we have to find the quadratic equation. To solve this, given a length and width of rectangle field using that find length and width of a rectangle path which around a given rectangular field and later by the formula of area of rectangle i.e.,
Complete step by step solution:
Given the measurement of the rectangular field i.e.,
Length of rectangle
Breadth of rectangle
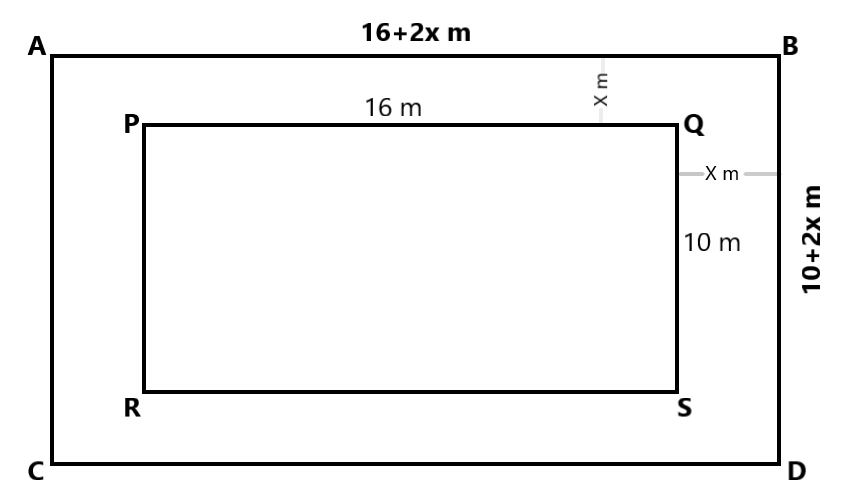
The path
Uniform width =
Length of rectangle
Breadth of rectangle
Area of rectangle
Area of rectangle
Area of rectangle
Area of rectangle
Now, by the formula of area of rectangle:
Subtract both side by 280, then
Or
Take out 4 as common, then
Divide both side by 4, then we get
The above equation resembles the equation
Therefore,
Note:
In the question they have mentioned the field in the rectangular shape so we consider the formula of area of rectangle. Suppose, if they mention any other plane figures we will consider the formula of respective plane figure. The quadratic equation is in the form of a polynomial equation whose degree is 2. Here, the unknown variables of the polynomial equation will represent the length and breadth of the rectangle.
Complete step by step solution:
Given the measurement of the rectangular field i.e.,
Length of rectangle
Breadth of rectangle

The path
Uniform width =
Length of rectangle
Breadth of rectangle
Area of rectangle
Area of rectangle
Area of rectangle
Area of rectangle
Now, by the formula of area of rectangle:
Subtract both side by 280, then
Or
Take out 4 as common, then
Divide both side by 4, then we get
The above equation resembles the equation
Therefore,
Note:
In the question they have mentioned the field in the rectangular shape so we consider the formula of area of rectangle. Suppose, if they mention any other plane figures we will consider the formula of respective plane figure. The quadratic equation is in the form of a polynomial equation whose degree is 2. Here, the unknown variables of the polynomial equation will represent the length and breadth of the rectangle.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




