Question

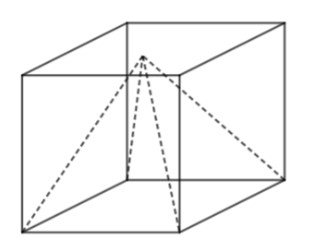
A regular square pyramid is placed in a cube so that the base of the pyramid and that of the cube coincide. The vertex of the pyramid lies on the face of the cube opposite to the base, as shown in the below. The edge of the cube is 7 inches. How many square inches (approximately) are in the positive difference between the surface area of the cube and the surface area of the pyramid?

(a) 452.6
(b) 158.6
(c) 294
(d) 135.4

Answer 1

Hint:First of all, find the area of the cube by using \[6{{\left( \text{side} \right)}^{2}}\]. Now, find the area of the regular square pyramid by using [(Area of the base + 4 (Area of the triangular faces)]. Here, the base would be the same as the base of the cube and the area of the triangle is \[\dfrac{1}{2}\times b\times h\]. Here b would be the side of the base of the pyramid and h would be its slant height. Find slant height by using the Pythagoras theorem. Finally, get the difference between the two surface areas.

Complete step-by-step answer:
We are given that a regular square pyramid is placed in a cube so that the base of the pyramid and that of the cube coincide. The vertex of the pyramid lies on the face of the cube opposite to the base, as shown in the below. And the edge of the cube is 7 inches. We have to find the number of square inches (approximately) that are in the positive difference between the surface area of the cube and the surface area of the pyramid.

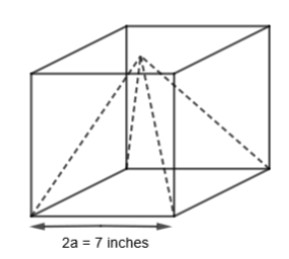
Let us assume the length of the sides of the cube as 2a. We know that the surface area of the cube is \[6{{\left( \text{side} \right)}^{2}}\]. So, we get, the surface area of the given cube
\[=6{{\left( 2a \right)}^{2}}\]
\[=24{{a}^{2}}....\left( i \right)\]
Also, we know that the base of the cube is square. So, we get,
Area of the base of the cube = Area of the base of the pyramid
\[={{\left( \text{side} \right)}^{2}}\]
\[={{\left( 2a \right)}^{2}}=4{{a}^{2}}\]
We are given that the vertex of the pyramid lies on the face of the cube opposite to the base. So, we get,
Height of the pyramid = side of the cube = 2a
We know that, in a pyramid, by using Pythagoras theorem, we get,
\[{{l}^{2}}={{\left( \dfrac{\text{side of the pyramid}}{2} \right)}^{2}}+{{\left( \text{height of the pyramid} \right)}^{2}}\]
where l is the slant height of the pyramid. So, we get,
\[{{l}^{2}}={{\left( \dfrac{2a}{2} \right)}^{2}}+{{\left( 2a \right)}^{2}}\]
\[{{l}^{2}}={{a}^{2}}+4{{a}^{2}}\]
\[l=\sqrt{5{{a}^{2}}}=a\sqrt{5}\]
We know that the surface area of the pyramid = (Area of the base of the Pyramid) + (Area of the 4 triangular faces of the Pyramid)
So, we get,
The surface area of the pyramid \[=4{{a}^{2}}+4\left( \text{area of 1 triangular face} \right)\]
\[=4{{a}^{2}}+4\left( \dfrac{1}{2}\times b\times h \right)\]
Here, b is the side of the base of the pyramid and h is the height, which is the slant height l, so we can substitute h = l.
\[=4{{a}^{2}}+4\dfrac{1}{2}\left( 2a\times \sqrt{5}a \right)\]
\[=4{{a}^{2}}+4\sqrt{5}{{a}^{2}}\]
\[=4{{a}^{2}}\left( 1+\sqrt{5} \right)....\left( ii \right)\]
So, we get the positive difference between the area of the cube and the pyramid = Area of the cube – Area of the pyramid.
By substituting the value of the area of the cube and the area of the pyramid from equation (i) and (ii) respectively, we get,
Difference between the areas \[=24{{a}^{2}}-4{{a}^{2}}\left( 1+\sqrt{5} \right)\]
\[=24{{a}^{2}}-4{{a}^{2}}-4\sqrt{5}{{a}^{2}}\]
\[=20{{a}^{2}}-4\sqrt{5}{{a}^{2}}\]
\[=4{{a}^{2}}\left( 5-\sqrt{5} \right)\]
We have assumed that 2a = 7 inches. So, a = 3.5 inches.
So, we get the difference between the areas
\[=4{{\left( 3.5 \right)}^{2}}\left[ 5-2.246 \right]\]
\[=135.4\text{ inche}{{\text{s}}^{2}}\]
Hence, option (d) is the right answer.

Note: In this question, while finding the surface area of the pyramid, in the area of the triangular face, many students take the height as 2a that is the height of the pyramid which is wrong because in the area of the triangle, \[\dfrac{1}{2}\times b\times h\], the base is the base of the triangle and height is the height of the triangle and here the height of the triangle is equal to the slant height of the pyramid, so that should be considered. So, this must be taken care of. Also, we took the sides as (2a) to avoid any fractions while doing the question because that leads to confusion.