Question

A satellite revolves in the geostationary orbit but in a direction east to west. The time interval between its successive passings about a point on the equator is:
A. 48hrs
B. 24hrs
C. 12hrs
C. Never

Answer 1

Hint: To solve this question we need to know that, when a satellite revolves in earth’s geostationary orbit, then the angular velocity of the satellite is the same as the angular velocity of earth. The relative angular velocity will be the sum of angular velocity of earth and angular velocity of the satellite.
And for a geostationary satellite, its time period (time taken to complete one rotation) is 24hrs.

Formula used:
Time period,
$T=\dfrac{2\pi }{\omega }$ .

Complete step-by-step answer:
In the question it is said that there is a satellite revolving in the geostationary orbit from east to west. We have to find the time interval between its successive passings about a point on the equator.

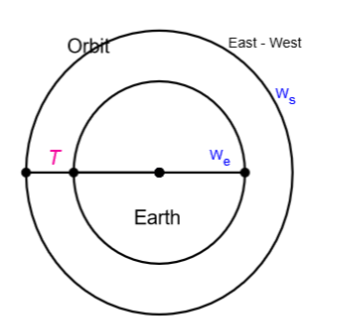
Consider earth as shown in the figure. The satellite is moving in an east west direction.
We know that earth has rotation. Therefore, let ${{\omega }_{e}}$ be the angular velocity of earth.
And let ${{\omega }_{s}}$ be the angular velocity of the satellite.
Let assume ‘T’ to be the time period between successive passings about the equator.
We know that, when a satellite is moving in the geostationary orbit of earth, its angular velocity is the same as that of earth’s angular velocity.
So we can write,
${{\omega }_{e}}={{\omega }_{s}}$
We have to find the time period of successive passing.
For that we have the equation of time period
$T=\dfrac{2\pi }{\omega }$
Here $\omega $ is relative angular velocity, which is equal to sum of angular velocities of earth and the satellite.
${{\omega }_{r}}={{\omega }_{e}}+{{\omega }_{s}}$
Therefore we rewrite T as
$\begin{align}
  & T=\dfrac{2\pi }{{{\omega }_{e}}+{{\omega }_{s}}} \\
 & T=\dfrac{2\pi }{2{{\omega }_{s}}} \\
 & T=\dfrac{1}{2}\left( \dfrac{2\pi }{{{\omega }_{s}}} \right) \\
\end{align}$
We know that,$\dfrac{2\pi }{{{\omega }_{s}}}$ is the time period of a geostationary satellite.
For geostationary satellite, time period T = 24hrs
Hence we can substitute this in the equation.
$\begin{align}
  & T=\dfrac{1}{2}\times 24 \\
 & T=12hrs \\
\end{align}$
Therefore the time interval between a geostationary satellite's successive passing about the equator is 12hrs.
Hence the correct answer is option C.

Note: A geostationary satellite is a satellite that orbits earth. It is placed directly above the earth’s equator. These satellites are used to provide visible and infrared images of earth’s surface. Most common communication satellites and broadcast satellites are orbiting in the geostationary orbit.