Question

A short bar magnet of magnetic moment 0.4J/T is placed in a uniform magnetic field of 0.10T. What is the potential energy when the magnet is stable?
(A $ -0.0\text{64} $ J
(B) ZERO
(C) -0.082 J
(D) 0.064 J

Answer 1

Hint : When a bar magnet is placed in a magnetic field, the two poles of the bar magnet experience equal to the opposite forces. In other words, at one end nullifies the force at the other end. Hence, the bar magnet experiences only the torque due to the magnetic field and there is no force.
Torque is the measure of the force that can cause an object to rotate about an axis.

FORMULA USED:
 $ \overrightarrow{\tau }=\overrightarrow{M}\times \overrightarrow{B} $
 $ \overrightarrow{B}= $ Magnetic field
 $ \overrightarrow{M}= $ Magnetic dipole moment
U = W
 $ =MB\left( \cos {{\theta }_{2}}-\cos {{\theta }_{1}} \right) $

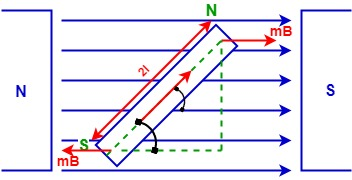
Complete step by step answer
When a magnetic dipole of moment M is held at an angle with the direction of a uniform magnetic field B, the magnitude of torque acting on the diploe is
 $ \overrightarrow{\tau }=\overrightarrow{M}\times \overrightarrow{B} $
 $ =MB\sin \theta $
This torque tends to align the dipole in the direction of the field. Work has to be done in rotating dipoles against the action of the torque. This work done is stored in the magnetic dipole as potential energy of the dipole.
Now, the small amount of work is done in rotating the dipole through a small angles $ d\theta $ is
 $ dW=\tau d\theta $
 $ =MB\sin \theta \cdot d\theta $
Total work done in rotating the dipole from $ \theta ={{\theta }_{1}}\text{ }to\text{ }\theta ={{\theta }_{2}}\text{ is:} $
 $ W=\int\limits_{{{\theta }_{1}}}^{{{\theta }_{2}}}{MB\sin \theta \cdot d\theta } $
 $ =MB\left| -\cos \theta \right|_{{{\theta }_{1}}}^{{{\theta }_{2}}} $
 $ W=-MB\left[ \cos {{\theta }_{2}}-\cos {{\theta }_{1}} \right] $ ……... (1)
When
 $ \text{ }{{\theta }_{1}}\text{ = 90}{}^\circ $ and $ {{\theta }_{2}}=\theta $
Then
U =W
 $ =-MB(\cos \theta -\cos 90{}^\circ ) $
= $ U=-MB\cos \theta $
In vector form;
 $ U=\overrightarrow{M}\centerdot \overrightarrow{B} $
When the magnet is in the stable equilibrium that is when the magnetic dipole is aligned along the magnetic field. The stable equilibrium has minimum potential energy.
When $ \theta =0{}^\circ $
 $ U=-MB\cos 0{}^\circ $
 $ U=-MB $ …..……... (2)
In our question the value of M and B are given as:
 $ M=0.4J{{T}^{-1}} $
 $ B=0.16T $
Put these values in equation (2)
 $ U=-(0.4)\times (0.16) $
 $ U=-0.064J $
Therefore option (A) is correct.

Note
Using the concept, we can also find out the value of U for unstable equilibrium, that is when $ \theta =180{}^\circ $ and expression becomes:
 $ U=-MB\cos 180{}^\circ $
 $ =-MB(-1) $
 $ U=MB $
 Having maximum potential energy.
Remember that when a bar magnet is placed in a uniform magnetic field it experiences only torque and no other force.