Question

A sinusoidal voltage of peak value 283V and frequency 50Hz is applied to a series LCR circuit in which $R = 3\Omega $, $L = 25.48mH$, $C = 786\mu F$.
Find
(a) The impedance of the circuit
(b) The phase difference between the voltage across the source and the current.
(c) The power factors.

Answer 1

Hint: This is a formula-based question. In this question, we have to find three things impedance of the circuit, phase difference, and power factors. The power factor of the LCR circuit can be defined as the ratio of resistance to the total impedance of the circuit. The total impedance can be denoted by (Z) and they consist of the magnitude of the phasor sum of resistance, inductive resistance, and capacitive resistance. At resonance, the inductive and capacitive resistances are equal.

Complete answer:

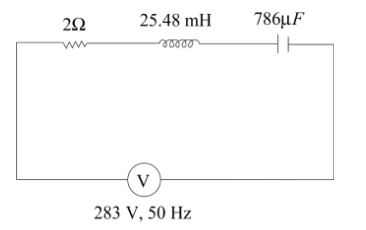
The formula used in this question are,
Power factor (p.f) =\[\dfrac{{\operatorname{Re} sis\tan ce(R)}}{{TotalImpedance\left( Z \right)}}\]
Total impedance (Z)=$\sqrt {\left( {\mathop R\nolimits^2 } \right) + \mathop {\left( {\mathop X\nolimits_C - \mathop X\nolimits_L } \right)}\nolimits^2 } $
Where $\mathop X\nolimits_C = $capacitive resistance $ = \dfrac{1}{{\omega c}}$
$\mathop X\nolimits_L $= inductive resistance =$\omega L$
Where $\omega = 2\pi f$
$f $ is the frequency of AC source
$C$ is capacitive circuit
$L$ is inductive circuit

The power factor can be defined as the ratio of resistance to the total impedance of the circuit The total impedance can consist of the inductive resistance, capacitive resistance, and the magnitude of the phasor sum of the resistance.
The power factor can be measured by the fraction of total power that can be used up or dissipated by a load resistor. The capacitor and inductor do not dissipate power.
If the power factor will be higher than energy efficiency will be better as a result greater fraction of the power is available for utilization.
At resonance, the frequency is
$\mathop X\nolimits_C = \mathop X\nolimits_L $
Firstly, we find the Angular Frequency of the AC signal
$\omega = 2\pi \nu $
$ \Rightarrow \omega = 2\pi \left( {50} \right) = 100\pi $
Then the capacitive resistance, $\mathop X\nolimits_C = \dfrac{1}{{\omega c}}$
$ \Rightarrow \mathop X\nolimits_C = \dfrac{1}{{100\pi \times 786 \times \mathop {10}\nolimits^{ - 6} }} = 4\Omega $
Then the inductive reactance is = $\mathop X\nolimits_L = \omega L$
$ \Rightarrow \mathop X\nolimits_L = 100\pi \times \left( {24.48 \times \mathop {10}\nolimits^{ - 3} } \right) = 8\Omega $
(a) The impedance of the circuit:
Total impedance (Z)=$\sqrt {\left( {\mathop R\nolimits^2 } \right) + \mathop {\left( {\mathop X\nolimits_C - \mathop X\nolimits_L } \right)}\nolimits^2 } $
$ \Rightarrow Z = \sqrt {{3^2} + {{\left( {8 - 4} \right)}^2}} = 5\Omega $
(b) The phase difference between the voltage across the source and the current:
Phase difference\[\left( \phi \right) = \mathop {\tan }\nolimits^{ - 1} \left( {\dfrac{{\mathop X\nolimits_L - \mathop X\nolimits_C }}{R}} \right)\]
On substituting the corresponding values, we get
$ \Rightarrow \phi = \mathop {\tan }\nolimits^{ - 1} \left( {\dfrac{{8 - 4}}{3}} \right) = \mathop {\tan }\nolimits^{ - 1} \left( {\dfrac{4}{3}} \right)$
$ \Rightarrow \phi = 53.13^\circ $
(c) The power factor:
 Power factor is denoted by cos $\phi $
So, power factor$ = \cos \phi = \cos 53.13^\circ $
Power factor= 0.6

$\therefore$ (a) Total impedance is $Z = \sqrt {{3^2} + {{\left( {8 - 4} \right)}^2}} = 5\Omega $
(b)The phase difference between the voltage across the source and the current is $\phi = 53.13^\circ $.
(c) Power factor is 0.6

Note:
At the stage of resonance, the LCR circuit behaves like a purely resistive circuit and the effects of the inductor and capacitor will cancel out each other. This circuit is the most efficient circuit in the operations. In these types of questions, firstly we have to remember all the formulas used and understand the meaning of RMS value and the terms such as impedance and reactance, then this type of question will be solved easily.