Question

A small bucket of mass $M$ is attached to a long inextensible cord of length $L$ . The bucket is released from rest when the cord is in a horizontal position. In its lowest position the bucket scoops up $m$ of water , what is the height of the swing above the lowest position?

Answer 1

Hint: We will first draw the diagram for the question first. Then we will find the velocity of the bucket when it touches the water. We will apply the law of conservation of energy in order to find the height of the swing above the lowest position.

Formula Used:
We will use the following formulae to solve this problem:-
$MgL=\dfrac{1}{2}M{{v}^{2}}$ .

Complete Step by Step Solution:
We have to draw the following diagram to get the answer:-

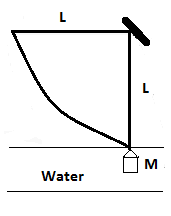
From the figure above we are going to analyse the problem properly.
We will get the speed of the bucket when it touches the water, this is also known as the lowest point. On applying law of principle of energy we get
$MgL=\dfrac{1}{2}M{{v}^{2}}$
$\Rightarrow {{v}^{2}}=2gL$
$v=\sqrt{2gL}$ ………….. $(i)$

Now, using the principle of conservation of linear momentum for the given case, using $(i)$ we have
$M\sqrt{2gL}=\left( M+m \right)v_{1}^{{}}$
$\Rightarrow {{v}_{1}}=\dfrac{M\sqrt{2gL}}{(M+m)}$ ………….. $(ii)$ (${{v}_{1}}$ is the velocity of bucket and water when the bucket scoops up )

Again applying conservation of energy we have
$\dfrac{1}{2}(M+m)v_{1}^{2}=(M+m)gh$
$\Rightarrow v_{1}^{2}=2gh$
$\Rightarrow {{v}_{1}}=\sqrt{2gh}$ ………….. $(iii)$

Now, equating equations $(ii)$ and $(iii)$ for the velocity ${{v}_{1}}$ we get,
$\dfrac{M\sqrt{2gL}}{\left( M+m \right)}=\sqrt{2gh}$ …………….. $(iv)$
Solving above equation further we get,
$h={{\left( \dfrac{M}{M+m} \right)}^{2}}L$.

Hence the correct answer for the height of the swing above the lowest point is, $h={{\left( \dfrac{M}{M+m} \right)}^{2}}L$ .

Additional Information:
Inextensible cord is a cord which can be pulled without being extended. Principle of conservation of linear momentum states that total momentum before collision and after collision is equal. That is, the total momentum of an isolated system is always constant. Conservation of energy states that energy can neither be created nor be destroyed but can only be transformed from one form into another.

Note:
We should apply the formula with care and without confusion. It is very important to use the principle of conservation of momentum at the correct position during the solution. We should not get confused between the law of conservation of energy and conservation of momentum.