Question

A square based pyramid has 5 faces and 5 vertices. Find the number of edges.
A. 6
B. 8
C. 10
D. 12

Answer 1

Hint: First of all, draw the figure of a given square based pyramid which is a three-dimensional polyhedron. Then use Euler's formula for finding the number of edges or calculate from the figure. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:

Given number of faces of square based pyramid F = 5
And the number of vertices of square based pyramid V = 5
Let the number of edges of square based pyramids be E.
The given square based pyramid is a three-dimensional polyhedron as shown in the figure:

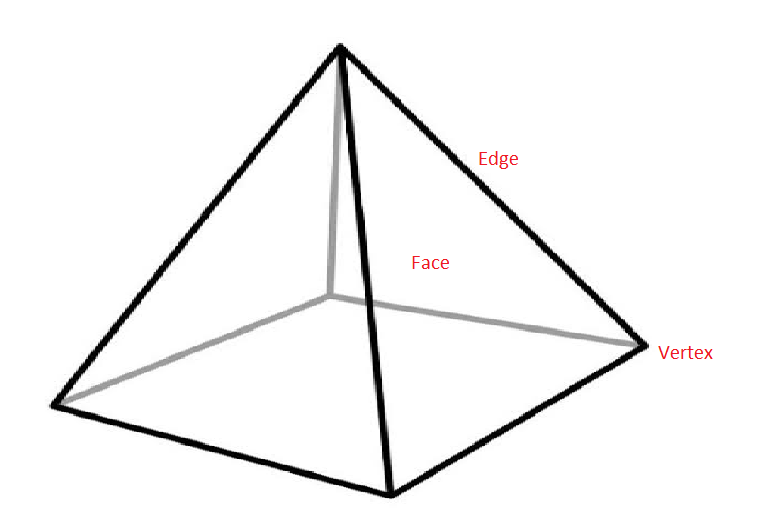
For any polyhedron, Euler`s formula tells us that the number of faces plus the number of vertices minus the number of edges equals 2. In other words: F + V – E = 2.
By using Euler`s formula and above data, we have
\[
   \Rightarrow F + V - E = 2 \\
   \Rightarrow 5 + 5 - E = 2 \\
   \Rightarrow 10 - E = 2 \\
   \Rightarrow E = 10 - 2 \\
  \therefore E = 8 \\
\]
Hence there are 8 edges in the square based pyramid.
Thus, the correct option is B. 8
Note: A polyhedron is a three dimensional solid that has flat faces. Two faces come together to form an edge. The corners of a polyhedron are called vertices. Euler`s formula is valid for all three-dimensional closed figures.