Question

A square has a perimeter of 12 centimeters. How do you find the length of the diagonal of the square?

Answer 1

Hint: We are given a square whose perimeter has 12cm, we are asked to find the length of the diagonal of the square. To do so, we will learn first about square, how are perimeter of square related to its side, then we learn how side are related to the diagonal, we will also use Pythagoras theorem ${{P}^{2}}={{B}^{2}}+{{H}^{2}}$ to solve our problem.

Complete step-by-step solution:
We are given a square whose perimeter is 12 cm.
We know that a square is a regular 4 sided polygon so all sides are equal.
Perimeter of any degree is the sum of all sides.
Since in square all sides are equal, so perimeter of square is $4\times sides.$
We are given perimeter of square as 12 cm so, perimeter $=12cm$ .
As we know $\text{Perimeter }=4\times \text{side}$ .
So, we get –
$4\times \text{side=12}$ (as perimeter $=12$ )
So, dividing both side by 4, we get –
$\dfrac{4\times \text{side}}{4}=\dfrac{12}{4}$
$\Rightarrow \text{side}=3$
So, we get a side of a square of 3cm.

Now, we have to find the length of the diagonal to do so we first see what one diagonal the line joining the opposite and of the vertex of the square are called as diagonal.

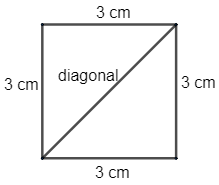
Now as we know SQUARE has ${{90}^{\circ }}$ angle at each vertex so sides and diagonal form a right angle triangle. We have a side of length 3cm and diagonal say D.

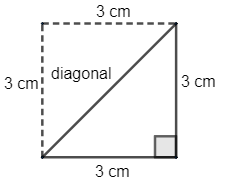
So, we will use Pythagoras theorem which say ${{P}^{2}}+{{B}^{2}}={{H}^{2}}$
We have Base $B=3$ and Perpendicular $P=3cm$ and hypotenuse as Diagonal D. So, we get –
${{D}^{2}}={{3}^{2}}+{{3}^{2}}$
As ${{3}^{2}}=9$ so,
${{D}^{2}}=9+9=18$ so,
${{D}^{2}}=18$
By simplifying, we get –
$\begin{align}
  & D=\sqrt{18} \\
 & =\sqrt{3\times 3\times 2} \\
\end{align}$
As 3 is making a pair, so it came out. We get –
$D=3\sqrt{2}cm$
Length of diagonal is $3\sqrt{2}cm$.

Note: We should be using Pythagoras theorem carefully it is always ${{P}^{2}}+{{B}^{2}}={{H}^{2}}$ , if we change the value as ${{P}^{2}}+{{H}^{2}}={{B}^{2}}$ or ${{P}^{2}}={{H}^{2}}+{{B}^{2}}$ or ${{P}^{2}}-{{B}^{2}}={{H}^{2}}$ , they all will lead us to get incorrect solution, also while finding diagonal we should remember length are always positive. So, ${{D}^{2}}=18\Rightarrow D=3\sqrt{2}$ , we do not discuss negative signs as it can never be an available option for length of diagonal.