Question

A stationary particle explodes into two particles of masses ${{m}_{1}}$ and ${{m}_{2}}$ which move in opposite direction with velocities ${{v}_{1}}$ and ${{v}_{2}}$. The ratio of the kinetic energies$\dfrac{{{E}_{1}}}{{{E}_{2}}}$ is
$\begin{align}
  & \text{A}\text{. }\dfrac{{{m}_{1}}}{{{m}_{2}}} \\
 & \text{B}\text{. 1} \\
 & \text{C}\text{. }\dfrac{{{m}_{1}}{{v}_{2}}}{{{m}_{2}}{{v}_{1}}} \\
 & \text{D}\text{. }\dfrac{{{m}_{2}}}{{{m}_{1}}} \\
\end{align}$

Answer 1

- Hint: First we will learn about Newton's third law. It states that for every action in nature there is an equal and opposite reaction. In other words, if object A exerts a force on object B, then object B also exerts an equal and opposite force on object A.

Complete step-by-step solution -

In the question it is given that the particle is stationary initially. Momentum of a particle is defined as the mass of the particle times its velocity. The particle’s initial velocity is 0. Hence, momentum will be zero. The explosion of the particle follows conservation of linear momentum principle. This states that, since no external force is acting on the particle, the momentum of the particle remains constant.

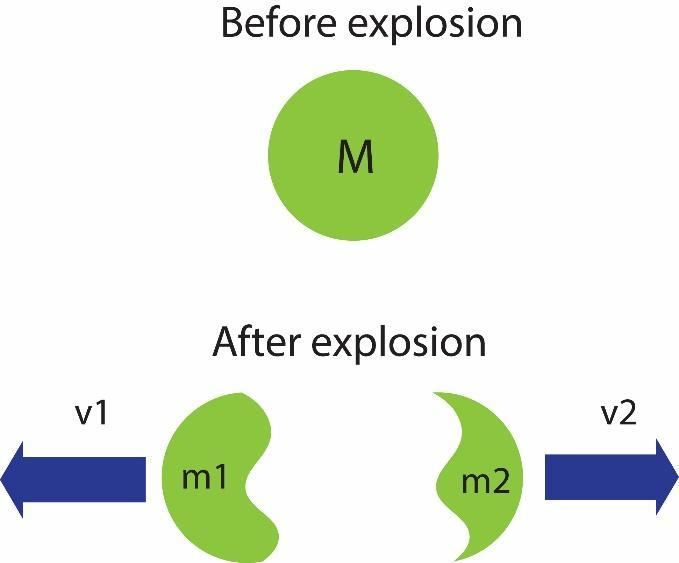
This means, after explosion, the total momentum is zero. The total momentum after explosion is given by,
$m_{1}{{v}_{1}}=m_{2}{{v}_{2}}$ . Here, the negative symbol is because the masses travel in opposite directions after the explosion. From, conservation of momentum, we can conclude that,
\[\begin{align}
  & m _{1}{{v}_{1}}=m_{2}{{v}_{2}} \\
 & \dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{{{v}_{2}}}{{{v}_{1}}}
\end{align}\] … (1)
The kinetic energy of a particle is defined by the energy that a particle contains due to its motion. The kinetic energy of a particle with mass m and velocity v is given by $\dfrac{1}{2}m{{v}^{2}}$.
The ratio of kinetic energies of masses ${{m}_{1}}$ and ${{m}_{2}}$,
 \[\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{\dfrac{1}{2}{{m}_{1}}{{v}_{1}}^{2}}{\dfrac{1}{2}{{m}_{2}}{{v}_{2}}^{2}}=\dfrac{{{m}_{1}}{{v}_{1}}}{{{m}_{2}}{{v}_{2}}}\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{{{m}_{2}}}{{{m}_{1}}}\]
In the above equation, \[\dfrac{{{m}_{1}}{{v}_{1}}}{{{m}_{2}}{{v}_{2}}}=1\] from equation (1).
Thus, the correct answer is D.

Note: This problem is solved using conservation of momentum principle which is a modification of Newton's third law. This is the main principle used in sending rockets to space.