Question

A straight line through origin O meets the parallel lines $4x+2y=9$ and $2x+y+6=0$ at point P and Q respectively. Then the point O divides the segment PQ in the ratio.
$\begin{align}
  & a)1:2 \\
 & b)3:4 \\
 & c)2:1 \\
 & d)4:3 \\
\end{align}$

Answer 1

Hint: Now we are given that a straight line through origin O meets the parallel lines $4x+2y=9$ and $2x+y+6=0$ at point P and Q respectively. We know that equation of line passing through origin is in $y=mx$ hence we will use this equation to solve with both lines to get the coordinates P and Q. Now we have coordinates of P, Q and O. hence we can use section formula which says if (x, y) divides the line joining $\left( {{x}_{1}},{{x}_{2}} \right)$ and $\left( {{y}_{1}},{{y}_{2}} \right)$ in ration m : n. then we have.
$\left( x,y \right)=\left( \left( \dfrac{m{{x}_{1}}+n{{x}_{2}}}{m+n} \right),\left( \dfrac{m{{y}_{1}}+n{{y}_{2}}}{m+n} \right) \right)$ . hence we can find the ratio m : n.

Complete step-by-step answer:

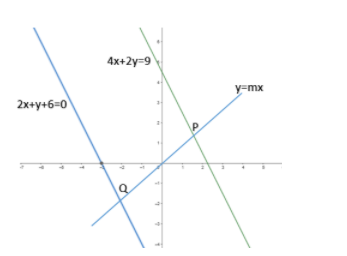
Now consider the equation of line passing through origin
We know that the equation of line passing through origin is $y=mx$
Now let us say the equation of line PQ is $y=mx$
Now Let us first find the point of intersection P.
P lies on line $4x+2y=9$ and the line $y=mx$
Now consider the line $4x+2y=9$
Dividing throughout by 2 we get
$2x+y=\dfrac{9}{2}$
Hence we get $y=\dfrac{9}{2}-2x$
Now at intersection point of line $4x+2y=9$ and the line $y=mx$ which is P we have
\[\begin{align}
  & mx=\dfrac{9}{2}-2x \\
 & mx+2x=\dfrac{9}{2} \\
 & x\left( m+2 \right)=\dfrac{9}{2} \\
 & x=\dfrac{9}{2\left( m+2 \right)}
\end{align}\]
Now substituting \[x=\dfrac{9}{2\left( m+2 \right)}\] in $y=mx$ we get.
$y=\dfrac{9m}{2\left( m+2 \right)}$
Hence the coordinates of P is $\left( \dfrac{9}{2\left( m+2 \right)},\left( \dfrac{9m}{2\left( m+2 \right)} \right) \right).............(1)$
Now line $2x+y+6=0$ and $y=mx$ intersects at Q.
Rearranging the terms of $2x+y+6=0$ we get $y=-2x-6$
Now at interaction point Q of line $2x+y+6=0$ and $y=mx$we will have
$mx=-2x-6$
Hence we get
$\begin{align}
  & mx+2x=6 \\
 & \Rightarrow x=\dfrac{6}{\left( m+2 \right)} \\
\end{align}$
Now substituting $x=\dfrac{6}{\left( m+2 \right)}$ in $y=mx$ we get $y=\dfrac{6m}{\left( m+2 \right)}$
Hence the coordinates of Q are $\left( \dfrac{6}{m+2},\dfrac{6m}{m+2} \right).....................(2)$
Now we have coordinates of P is $\left( \dfrac{9}{2\left( m+2 \right)},\left( \dfrac{9m}{2\left( m+2 \right)} \right) \right)$ and coordinates of Q are $\left( \dfrac{6}{m+2},\dfrac{6m}{m+2} \right)$
Now we have O = (0, 0) divides the line PQ internally.
Let us say that that the point O divides the line PQ in ratio λ : 1.
Then we know by section formula if (x, y) divides the line joining $\left( {{x}_{1}},{{x}_{2}} \right)$ and $\left( {{y}_{1}},{{y}_{2}} \right)$ in ration m : n. then we have.
$\left( x,y \right)=\left( \left( \dfrac{m{{x}_{1}}+n{{x}_{2}}}{m+n} \right),\left( \dfrac{m{{y}_{1}}+n{{y}_{2}}}{m+n} \right) \right)$
Hence for the line PQ we have.
$\left( 0,0 \right)=\left( \dfrac{\left( \dfrac{\lambda 9}{2\left( m+2 \right)}-\dfrac{6}{m+2} \right)}{\lambda +1},\dfrac{\left( \dfrac{\lambda 9m}{2\left( m+2 \right)}-\dfrac{6m}{m+2} \right)}{\lambda +1} \right)$
Now first equating x coordinate we get
\[\begin{align}
  & \dfrac{\left( \dfrac{\lambda 9}{2\left( m+2 \right)}-\dfrac{6}{m+2} \right)}{\lambda +1}=0 \\
 & \Rightarrow \left( \dfrac{\lambda 9}{2\left( m+2 \right)}-\dfrac{6}{m+2} \right)=0 \\
 & \Rightarrow \dfrac{\lambda 9}{2\left( m+2 \right)}=\dfrac{6}{m+2} \\
 & \Rightarrow \dfrac{3\lambda }{2}=\dfrac{2}{1} \\
 & \Rightarrow \lambda =\dfrac{4}{3} \\
\end{align}\]
Hence the value of λ is $\dfrac{4}{3}$ .
Now we have point O divides the line PQ in ratio λ : 1.
Hence O divides PQ in $\dfrac{4}{3}:1=4:3$
Hence we have O divides line PQ in 4 : 3.
Option d is the correct answer.

Note: In section formula we use the ratio as m : n, and to solve we have assumed the ratio to be λ : 1 for simplicity. The answer through both the methods will be the same.