Question

A tank with a small hole at the bottom has been filled with water and kerosene (specific gravity \[0.8\]). The height of water is \[3m\] and that of kerosene \[2m\]. When the hole is opened the velocity of fluid coming out from it is nearly: (take\[g=10m/{{s}^{2}}\]) and density of water\[{{10}^{3}}Kg/{{m}^{3}}\])

A \[8.5\text{ }m/s\]
B \[9.6\text{ }m/s\]
C \[10.7\text{ }m/s\]
D \[7.6\text{ }m/s\]

Answer 1

Hint: Here, it is asked to determine the velocity of fluid coming out of the hole. To find out the velocity of fluid flow from an orifice we can use the Bernoulli’s theorem which states that, per unit mass of an incompressible, non-viscous fluid in a streamlined flow, the sum of pressure energy, kinetic energy, and potential energy remains a constant. Here, density and height of water, specific gravity and height of kerosene are given. By substituting it in Bernoulli’s equation, we can find out the velocity.
Formula used:
\[\text{Density of a fluid = specific gravity of fluid }\!\!\times\!\!\text{ density of water}\]
\[{{\text{P}}_{1}}+\dfrac{1}{2}\rho v_{1}^{2}+\rho g{{h}_{1}}={{\text{P}}_{2}}+\dfrac{1}{2}\rho v_{2}^{2}+\rho g{{h}_{2}}\]
\[{{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}\]

Complete answer:
Given,
\[\text{Density of water, }{{\rho }_{w}}\text{ = 1}{{\text{0}}^{\text{3}}}\text{Kg/}{{\text{m}}^{\text{3}}}\]
\[g=10m/{{s}^{2}}\]
\[\text{Height of water, }{{\text{h}}_{w}}\text{ = 3m}\]
\[\text{Height of kerosene, }{{\text{h}}_{k}}\text{ = 2m}\]
\[\text{Specific gravity of kerosene = 0}\text{.8}\]
We have,
\[\text{Density of a fluid = specific gravity of fluid }\!\!\times\!\!\text{ density of water}\]
Then,
\[\text{Density of kerosene, }{{\rho }_{k}}\text{ = 0}\text{.8 }\!\!\times\!\!\text{ 1000=800}\]

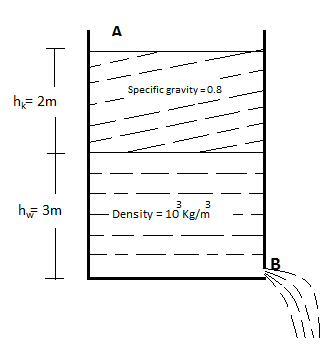
We have Bernoulli’s equation,
\[{{\text{P}}_{1}}+\dfrac{1}{2}\rho v_{1}^{2}+\rho g{{h}_{1}}={{\text{P}}_{2}}+\dfrac{1}{2}\rho v_{2}^{2}+\rho g{{h}_{2}}\] --------- 1
Here we have,
\[{{P}_{1}}={{P}_{2}}={{P}_{0}}\](Both the points are open to atmosphere) ------- 2
\[\rho ={{\rho }_{k}}+{{\rho }_{w}}\] ------- 3
\[{{\text{h}}_{\text{1}}}\text{= }{{\text{h}}_{w}}+{{h}_{k}}\] ------- 4
Since the hole is at the bottom of tank,
\[{{h}_{2}}=0\] -------- 5
When hole is opened, fluid coming out from the hole will be water. Hence, we need to use the formula for kinetic energy of water in equation 1.
Apply Bernoulli’s theorem at point A and B. And substitute 2, 3, 4, 5 and 6 in equation 1 we get,
\[{{\text{P}}_{0}}+\dfrac{1}{2}{{\rho }_{w}}v_{1}^{2}+\left( {{\rho }_{w}}g{{h}_{w}}+{{\rho }_{k}}g{{h}_{k}} \right)={{\text{P}}_{0}}+\dfrac{1}{2}{{\rho }_{w}}v_{2}^{2}\] --------- 7
Applying continuity equation at the hole and at the top of tank,
\[{{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}\]
Where,
\[{{\text{A}}_{\text{1}}}\text{- Area of the top portion}\]
\[{{\text{A}}_{2}}\text{- Area of hole}\]
\[{{v}_{\text{1}}}\text{- Velocity of the fluid at point A}\]
\[{{v}_{2}}\text{- Velocity of the fluid at point B}\]
Here, \[{{\text{A}}_{\text{1}}}\] is much greater than \[{{\text{A}}_{2}}\]
Then,
\[{{v}_{1}}\approx 0\]
Substituting the values of \[{{\text{h}}_{\text{1}}}\text{,}{{\text{h}}_{\text{2}}}\text{,}{{\text{ }\!\!\rho\!\!\text{ }}_{k}}\text{,}{{\rho }_{w}}\text{,g and }{{\text{v}}_{1}}\] in equation 7, we get,
\[3\times {{10}^{3}}\times 10+2\times 0.8\times {{10}^{3}}\times 10=\dfrac{1}{2}\times {{10}^{3}}\times v_{2}^{2}\]
\[v_{2}^{2}=92\]
\[{{v}_{2}}=\sqrt{92}=9.6m/s\]

So, the correct answer is “Option B”.

Note:
When two fluids with different densities are mixed, denser fluid will settle at the bottom. Here the water has a density higher than kerosene. Hence water settles at the bottom and when the hole is opened, water starts flowing out first.