Question

A tetrahedron has 4 faces and 6 edges. How many vertices does it have?
(a). 2
(b). 4
(c). 6
(d). 8

Answer 1

Hint: We have a tetrahedron that has four faces and 6 edges. We have to find the number of vertices. Use the Euler’s polyhedron formula, \[V-E+F=2\] , where V is the number of vertices, e is the number of edges and F is the number of faces. Now, solve further and the value of V, which is the number of vertices.

Complete step-by-step answer:

According to the question, it is given that a tetrahedron has 4 faces and 6 edges. We are required to find the exact number of vertices of the tetrahedron.
We know that tetrahedron is a form of a polyhedron. So, we can apply Euler’s polyhedron formula here.
According to Euler’s polyhedron formula, we have
\[V-E+F=2\] …………….(1)
, where V is the number of vertices, e is the number of edges and F is the number of faces.
In a tetrahedron,
Number of faces = 4 ……………………(2)
Number of edges = 6 …………………..(3)
From equation (1), equation (2) and equation (3), we get
\[\begin{align}
  & V-E+F=2 \\
 & \Rightarrow V-6+4=2 \\
\end{align}\]
On solving, we get
\[\begin{align}
  & \Rightarrow V=2+2 \\
 & \Rightarrow V=4 \\
\end{align}\]
Hence, the number of vertices is 4.
Therefore, option (B) is the correct one.

Note: One can also solve this question with the help of a figure of tetrahedron. We have the point E,F, and G in the vertical plane and point H coming out of the plane EFG.

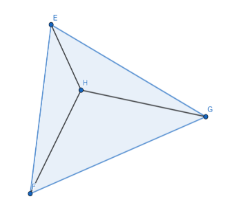
In this figure, we have plane EFG, EHF, EHG, and FHG as the face of the tetrahedron and EF, EG, EH, FG, FH, and GH as the edges of the tetrahedron. Points E, F, G, and H are the vertices of the tetrahedron.
Hence, the number of vertices is 4.
But don’t proceed with this approach because it is very difficult to imagine the figure if the given polyhedron is octahedron or something else complex.