Question

A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at $\left( {{\text{0,}}0} \right)$ and the object is placed at $\left( { - 50{\text{cm,}}0} \right)$. Find the coordinates of the image.

Answer 1

Hint: From the coordinates of the object we see that the object is placed at a point corresponding to $2{F_1}$ on the principal axis. A convex lens produces an inverted image of the same size when the object is at this point on the principal axis. A ray diagram showing the image formation by the top part of the convex lens will provide better understanding.

Formulas used:
The thin lens equation is given by, $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ where $v$ is the image distance, $u$ is the object distance and $f$ is the focal length of the lens.
The magnification of a lens is given by, $m = \dfrac{{h'}}{h} = \dfrac{v}{u}$ where $h$, $h$‘ are the sizes of the object and image respectively and $v$, $u$ are the image distance and object distance respectively.

Complete step by step answer:
Step 1: Sketch a diagram of the convex lens before and after cutting it into pieces.

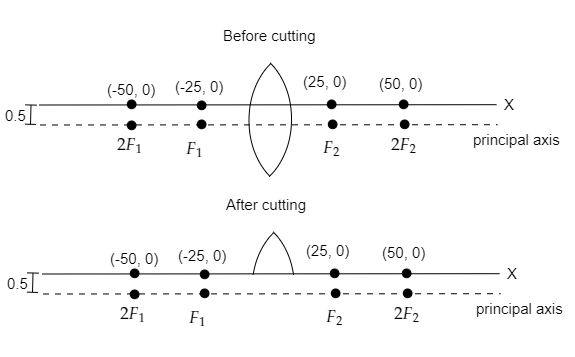
After cutting only the top part is placed at the origin of the x-axis.
Step 2: Sketch a ray diagram for the image formed when the object is placed at $\left( { - 50{\text{cm,}}0} \right)$.
A ray parallel to the principal axis, on refraction, will pass through the focal point on the other side of the lens and a ray passing through the optical center will emerge unrefracted.
Rays from the tip of the object and bottom of the object are sketched to get the size of the image.

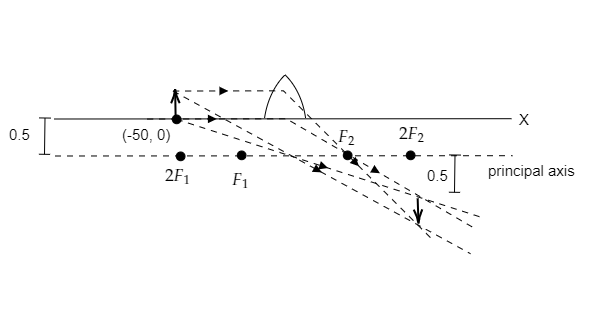
In the above diagram, the object is placed at $\left( { - 50{\text{cm,}}0} \right)$ i.e., $u = - 50{\text{cm}}$.
The focal length of the lens is given to be $f = 25{\text{cm}}$. So the object is placed at a point corresponding to $2{F_1}$ on the principal axis. We know that for a convex lens when an object is placed at $2{F_1}$ then the image will be formed at $2{F_2}$.
So the X-coordinate of the image will be 50 cm.
As the image and the object are of the same size, the image will be formed at a distance of 0.5 cm below the principal axis which lies at a distance of 0.5 cm below the x-axis. Then the Y-coordinate of the image will be
$\Rightarrow - 0.5 - 0.5 = - 1{\text{cm}}$.

Thus the coordinate of the image will be $\left( {50{\text{cm,}} - {\text{1cm}}} \right)$.

Note:
Alternate method:
The object distance is given to be $u = - 50{\text{cm}}$ and the focal length of the lens is $f = 25{\text{cm}}$.
The X- coordinate of the image can be obtained by the thin lens equation given by,
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ or $\dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u}$ -------- (1)
Substituting the values for $u = - 50{\text{cm}}$ and $f = 25{\text{cm}}$ in equation (1) we get,
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{25}} - \dfrac{1}{{50}} = \dfrac{1}{{50}}$
Then the X-coordinate of the image will be $v = 50{\text{cm}}$.
The Y-coordinate of the image is obtained by the relation for the magnification of the lens given by, $m = \dfrac{{h'}}{h} = \dfrac{v}{u}$ --------- (2)
Substituting for $u = - 50{\text{cm}}$ and $v = 50{\text{cm}}$ in equation (2) we get,
$\Rightarrow m = \dfrac{{50}}{{ - 50}} = - 1$
So the image is inverted. The size of the object is $h = 0.5{\text{cm}}$
Then from (2), we have
$\Rightarrow h' = hm = - 1 \times 0.5 = - 0.5{\text{cm}}$
Thus the image will be formed 0.5 cm below the principal axis. Since the principal axis is 0.5 cm below the x-axis, the image will be formed 1 cm below the x-axis.
Thus the coordinate of the image will be
$\Rightarrow \left( {50{\text{cm,}} - {\text{1cm}}} \right)$.