Question

A toy company manufactures two types of doll; a basic version doll A and a deluxe version doll B. Each doll of type B takes twice as long to produce as one of type A and the company would have time to make a maximum of 2000 dolls of type A per day. The supply of plastic is sufficient to produce 1500 dolls per day and each type requires an equal amount of each. The deluxe version requires a fancy dress of which there are only 600 per day available. If the company makes profit Rs. 3 and Rs. 5 per doll respectively for doll A and doll B; how many of each should be produced per day in order to maximize profit? Solve it by graphical method.

Answer 1

Hint:
We will formulate inequalities based on the information given in the question and the function that has to be maximized. We will represent these inequalities on the graph and find the feasible region that is satisfying all these inequalities. We will find all the corner points of the feasible region. We will substitute these points in the objective function and find which point gives the maximum function value. That point will be the solution to our problem.

Complete step by step solution:
We will assume that the number of dolls of type A is \[x\] and the number of dolls of type B is \[y\].
We know that each doll of type B takes twice as long to produce as type A and the company can make a maximum of 2000 dolls of type A per day.
So we can express the statement as,
\[x + 2y \le 2000\]
We know that the plastic supply is enough to make 1500 dollars per day. So we can express the statement as,
\[x + y \le 1500\]
We know that only 600 fancy dresses are available for type B. So we can express the statement as,
\[y \le 600\]
We know that the number of dolls cannot be negative.
Therefore,
\[x,y \ge 0\]
We know that the profit on doll A is Rs. 3 and the profit on doll B is Rs. 5. We need to maximize the profit:
\[{\rm{Max}}:z = 3x + 5y\]
To plot an inequality, we will first draw the line that it represents and then we will shade the region towards a point that satisfies the inequality. For example, the point (0, 0) satisfies the inequality \[x + 2y \le 2000\], so we will draw the line \[x + 2y = 2000\] and shade the region towards the origin.
We will plot all the inequalities on the graph:

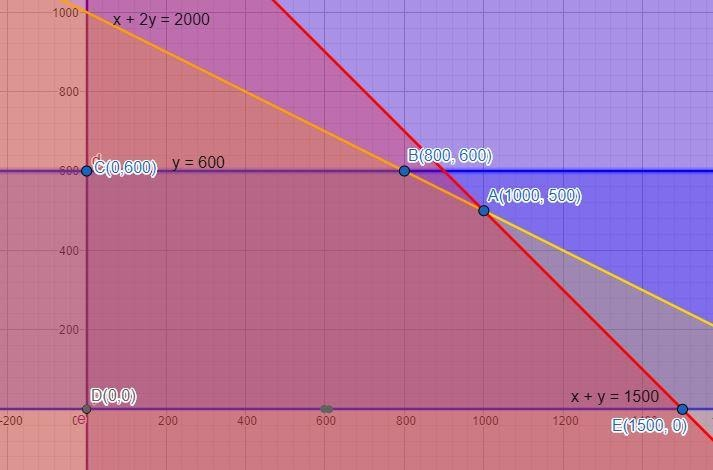
We can see from the graph that the region defined by polygon ABCDE is the feasible region for our problem. We will find the corner points of this region by finding the points of intersection of the lines. They are:
\[\begin{array}{l}A\left( {1000,500} \right)\\B\left( {800,600} \right)\\C\left( {0,600} \right)\\D\left( {0,0} \right)\\E\left( {1500,0} \right)\end{array}\]
We will put the values of these points in the \[\max :z = 3x + 5y\] function and find its value for each point:
\[\begin{array}{l}A\left( {1000,500} \right):z = 3\left( {1000} \right) + 5\left( {500} \right)\\{\rm{ }} = 5500\end{array}\]
\[\begin{array}{l}B\left( {800,600} \right):{\rm{ }}z = 3\left( {800} \right) + 5\left( {600} \right)\\{\rm{ }} = 5400\end{array}\]
\[\begin{array}{l}C\left( {0,600} \right):{\rm{ }}z = 3\left( 0 \right) + 5\left( {600} \right)\\{\rm{ }} = 3000\end{array}\]
\[\begin{array}{l}D\left( {0,0} \right):{\rm{ }}z = 3\left( 0 \right) + 5\left( 0 \right)\\{\rm{ }} = 0\end{array}\]
\[\begin{array}{l}E\left( {1500,0} \right):{\rm{ }}z = 3\left( {1500} \right) + 5\left( 0 \right)\\{\rm{ }} = 4500\end{array}\]
We can see that the profit is maximum at \[A\left( {1000,500} \right)\].

$\therefore $ 1000 dolls of type A and 500 dolls of type B should be produced per day to maximize the profit.

Note:
When we graph an inequality, if the inequality sign is less than equal to \[\left( \le \right)\] or greater than equal to \[\left( \ge \right)\], we should draw a solid line to represent the region but if the inequality sign is only less than \[\left( < \right)\] or greater than \[\left( > \right)\], we should draw a dotted line to represent the region. The dotted line signifies that the straight line is not a part of the feasible region.