
A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed \[1200\] dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other types by at most \[600\] units. If the company makes a profit of Rs. 12 and Rs.16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximize the profit?
Answer
561k+ views
Hint: Here, first we have to formulate the given problem into mathematical equations with the given conditions. Then, we will solve these equations using the linear programming graphical method. The values of variables that have the maximum profit will be the production of both types of dolls A and B respectively. Linear programming or LP is a method or a process to achieve the best outcome such as maximum profit or lowest cost in a mathematical model where the requirements are represented by linear relationships.
Complete step by step solution:
Let \[x\] be the dolls of type A manufactured by a toy company and \[y\] be the dolls of type B manufactured by a toy company.
Since the market tests and available resources have indicated that the combined production level should not exceed \[1200\] dolls per week. Therefore, we get
\[x + y \le 1200\] ……………….. \[\left( 1 \right)\]
It is given that the demand for dolls of type B is at most half of that for dolls of type A, then
\[y \le \dfrac{x}{2}\]
Or we can write,
\[ \Rightarrow 2y - x \le 0\] …………………..\[\left( 2 \right)\]
We know that the production level of dolls of type A can exceed three times the production of dolls of other types by at most \[600\] units.
\[ \Rightarrow x - 3y \le 600\]…..……………\[\left( 3 \right)\]
Since it is not possible to produce negative quantities, we have \[x \ge 0\] and \[y \ge 0\].
The objective is to maximize the profit, so the total profit is given by the relation
\[ \Rightarrow z = 12x + 16y\]………………\[\left( 4 \right)\]
Therefore the constraints are \[x + y = 1200;2y - x = 0;x - 3y = 600;x \ge 0\] and \[y \ge 0\] .
The \[x\] intercept and \[y\] intercept of the equation \[\left( 1 \right)\] are \[y = 1200\] and \[x = 1200\] .
The \[x\] intercept and \[y\] intercept of the equation \[\left( 3 \right)\] are \[y = - 200\] and \[x = 600\] .
Now, we have to solve the equations \[\left( 1 \right)\] and \[\left( 2 \right)\], we have \[x = 800\] and \[y = 400\].
Now we will draw the graph using the constraints.
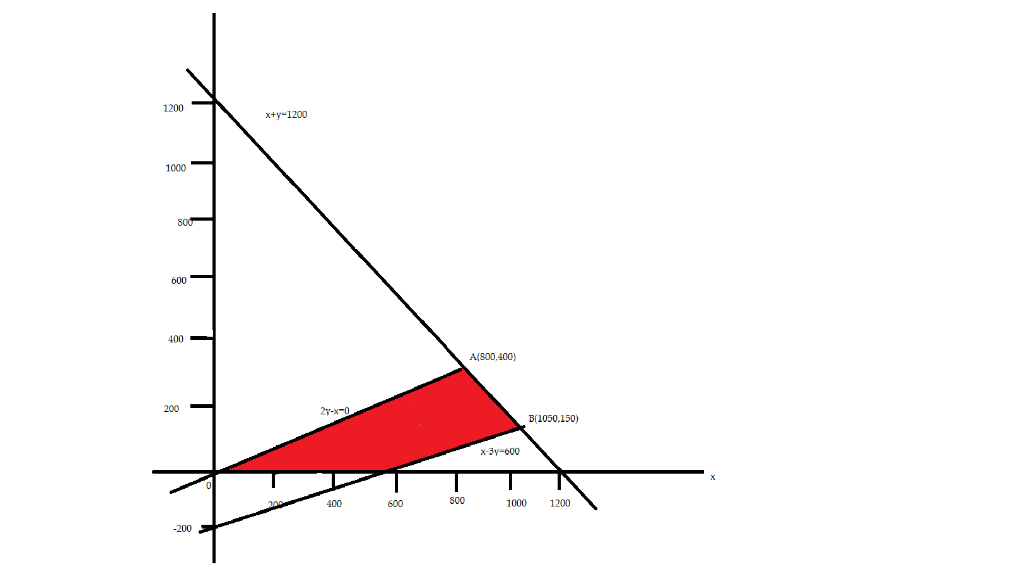
The intersection points of the constraints forming a closed region are the feasible region.
Now we will form the table and substitute the values of \[x\] and \[y\] in the constraints to find the maximum amount.
The total profit or the maximum amount is Rs. 16000. So the company should produce 800 dolls of Type A and 400 dolls of Type B to maximize the profit.
Note: To solve a system of linear equations by the graphical method, we need to draw the graph for each of the equations and check for a point of intersection between any two graphs. The coordinates of the point of intersection would be the solution to the system of equations. According to the graphical method, when there is no intersection then there is no solution.
Complete step by step solution:
Let \[x\] be the dolls of type A manufactured by a toy company and \[y\] be the dolls of type B manufactured by a toy company.
Since the market tests and available resources have indicated that the combined production level should not exceed \[1200\] dolls per week. Therefore, we get
\[x + y \le 1200\] ……………….. \[\left( 1 \right)\]
It is given that the demand for dolls of type B is at most half of that for dolls of type A, then
\[y \le \dfrac{x}{2}\]
Or we can write,
\[ \Rightarrow 2y - x \le 0\] …………………..\[\left( 2 \right)\]
We know that the production level of dolls of type A can exceed three times the production of dolls of other types by at most \[600\] units.
\[ \Rightarrow x - 3y \le 600\]…..……………\[\left( 3 \right)\]
Since it is not possible to produce negative quantities, we have \[x \ge 0\] and \[y \ge 0\].
The objective is to maximize the profit, so the total profit is given by the relation
\[ \Rightarrow z = 12x + 16y\]………………\[\left( 4 \right)\]
Therefore the constraints are \[x + y = 1200;2y - x = 0;x - 3y = 600;x \ge 0\] and \[y \ge 0\] .
The \[x\] intercept and \[y\] intercept of the equation \[\left( 1 \right)\] are \[y = 1200\] and \[x = 1200\] .
The \[x\] intercept and \[y\] intercept of the equation \[\left( 3 \right)\] are \[y = - 200\] and \[x = 600\] .
Now, we have to solve the equations \[\left( 1 \right)\] and \[\left( 2 \right)\], we have \[x = 800\] and \[y = 400\].
Now we will draw the graph using the constraints.

The intersection points of the constraints forming a closed region are the feasible region.
Now we will form the table and substitute the values of \[x\] and \[y\] in the constraints to find the maximum amount.
| Co-ordinates | Maximize \[z = 12x + 16y\] | Amount |
| A\[(800,400)\] | \[z = 12(800) + 16(400)\] | 16000 |
| B\[(1050,150)\] | \[z = 12(1050) + 16(150)\] | 15000 |
| C\[( - 600,200)\] | \[z = 12(600) + 16( - 200)\] | 4400 |
| D\[(0,0)\] | \[z = 12(0) + 16(0)\] | 0 |
The total profit or the maximum amount is Rs. 16000. So the company should produce 800 dolls of Type A and 400 dolls of Type B to maximize the profit.
Note: To solve a system of linear equations by the graphical method, we need to draw the graph for each of the equations and check for a point of intersection between any two graphs. The coordinates of the point of intersection would be the solution to the system of equations. According to the graphical method, when there is no intersection then there is no solution.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

A Paragraph on Pollution in about 100-150 Words

State and prove the Pythagoras theorem-class-10-maths-CBSE




