Question

A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other types by at most 600 units. If the company makes a profit of Rs.12 and Rs.16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximize the profit?

Answer 1

Hint: We first transform the given conditions into their mathematical forms. We find four different inequalities. We use them in the graph to find the common area. We take the extremum points and try to find the maximum profit out of those. The maximum output will be the final answer.

Complete step by step answer:
Let's assume that the number of dolls of type A is x and the number of dolls of type B be y.
Value of x and y can’t be negative. So, $x,y\ge 0....(i)$.
Since combined production level should not exceed 1200 dolls per week.
We get a linear inequation according to the conditions which is \[x+y\le 1200~....(ii)\]
Since the production levels of dolls of type A exceeds 3 times the production of type B by at most 600 units, we also express this condition in mathematical form as \[x-3y\le 600....(iii)\]
Also, the demands of dolls of type B is at most half of that for dolls of type A which gives us \[\begin{align}
  & y\le \dfrac{x}{2} \\
 & \Rightarrow 2y-x\le 0.....(iv) \\
\end{align}\]
Now, profit on type A dolls is Rs 12 and profit on type B dolls is Rs 16.
We express the total profit in its equational form where z is the total profit $z=12x+16y$.
We have to maximize the total profit (z) of the manufacturers.
We have four inequalities to find the required area in the graph.
After plotting all the constraints given by equation (i), (ii), (iii) and (iv) we get the feasible region as shown in the image.

Now we take the corner points to find out the maximum.

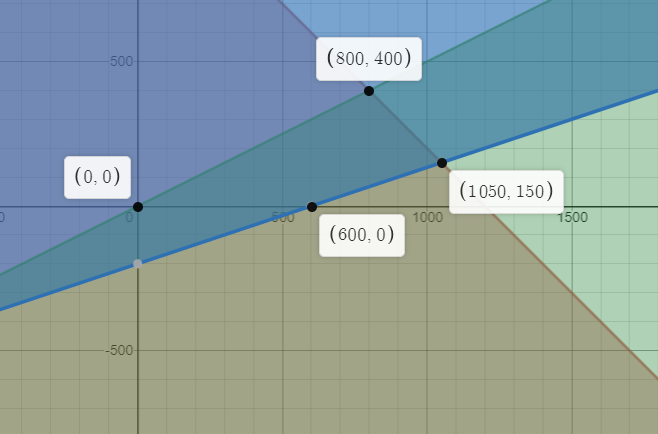
There are 4 corner point values.
$A\equiv \left( 0,0 \right),B\equiv \left( 600,0 \right),C\equiv \left( 1050,150 \right),D\equiv \left( 800,400 \right)$.
We find the equational value of $z=12x+16y$ for these four points.
At $A\equiv \left( 0,0 \right)$, $z=12x+16y=0+0=0$.
At $B\equiv \left( 600,0 \right)$, $z=12x+16y=12\times 600+0=7200$.
At $C\equiv \left( 1050,150 \right)$, $z=12x+16y=12\times 1050+16\times 150=15000$.
At $D\equiv \left( 800,400 \right)$, $z=12x+16y=12\times 800+16\times 400=16000$.
The maximum one is at $D\equiv \left( 800,400 \right)$.

So, in order to maximize the profit, the company should produce 800 type A dolls and 400 type B dolls

Note: We don’t need to consider the whole area. The extremum points or the intersecting points are the points or data to consider for maximized profit. The inequality $x,y\ge 0....(i)$ gives us the whole first quadrant. We don’t need to map out this in the graph.