Question

A triangle ABC is placed so that the mid-points of the sides are on the x,y,z axes. Lengths of the intercepts made by the plane containing the triangle on these axes are respectively \[\alpha ,\beta ,\gamma \]. Coordinates of the centroid of the triangle ABC are
A. \[( - \alpha /3,\beta /3,\gamma /3)\]
B. \[(\alpha /3, - \beta /3,\gamma /3)\]
C. \[(\alpha /3,\beta /3, - \gamma /3)\]
D. \[(\alpha /3,\beta /3,\gamma /3)\]

Answer 1

Hint: A triangle ABC is placed so that the mid-points of the sides are on the x,y,z axes. Lengths of the intercepts made by the plane containing the triangle on these axes are respectively\[\alpha ,\beta ,\gamma \]. Coordinates of the centroid of the triangle ABC are
\[( - \alpha /3,\beta /3,\gamma /3)\]
\[(\alpha /3, - \beta /3,\gamma /3)\]
\[(\alpha /3,\beta /3, - \gamma /3)\]
\[(\alpha /3,\beta /3,\gamma /3)\]

Complete step by step solution:
1) \[\,ABC\] is placed so that the mid-points of the sides are on the x,y,z axes
i.e.:D,E,F are the mid-points of CA , BC , BA respectively and D,E,F lie on the Z,Y,X axes.
2) Lengths of the intercepts made by the plane containing the triangle on these axes are \[\alpha ,\beta ,\gamma \]respectively which means the coordinates of D,E,F are \[F(\alpha ,0,0),E(0,\beta ,0)and\,D(0,0,\gamma )\].

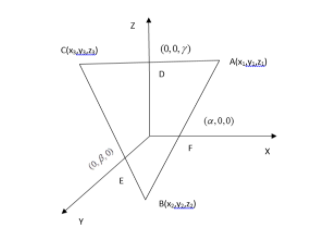
Here, \[A = ({x_1},{y_1},{z_1})\]
          \[B = ({x_2},{y_2},{z_2})\]
          \[C = ({x_3},{y_3},{z_3})\]
     And \[F = (\alpha ,0,0)\]
          \[E = (0,\beta ,0)\]
          \[D = (0,0,\gamma )\]
Step 1: To make a relation between the coordinates of A,B,C with \[\alpha ,\beta ,\gamma \]
i)= > \[F = (\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2},\dfrac{{{z_1} + {z_2}}}{2})\] [ F is the mid point of AB]
= > \[F = (\alpha ,0,0)\]
i.e.: \[\dfrac{{{x_1} + {x_2}}}{2} = \alpha ,\,\,\dfrac{{{y_1} + {y_2}}}{2} = 0,\,\,\dfrac{{{z_1} + {z_2}}}{2} = 0\]
ii) = > \[E = (\dfrac{{{x_2} + {x_3}}}{2},\dfrac{{{y_2} + {y_3}}}{2},\dfrac{{{z_2} + {z_3}}}{2})\] [ E is the mid point of BC]
= > \[F = (0,\beta ,0)\]
i.e.: \[\dfrac{{{x_2} + {x_3}}}{2} = 0,\,\,\dfrac{{{y_2} + {y_3}}}{2} = \beta ,\,\,\dfrac{{{z_2} + {z_3}}}{2} = 0\]
=> \[D = (\dfrac{{{x_3} + {x_1}}}{2},\dfrac{{{y_3} + {y_1}}}{2},\dfrac{{{z_3} + {z_1}}}{2})\]
= > \[D = (0,0,\gamma )\]
i.e.: \[\dfrac{{{x_3} + {x_1}}}{2} = 0,\,\,\dfrac{{{y_3} + {y_1}}}{2} = 0,\,\,\dfrac{{{z_3} + {z_1}}}{2} = \gamma \]
From (i) , We get,
\[{x_1} + {x_2} = 2\alpha \]
\[{y_1} + {y_2} = 0\]
\[{z_1} + {z_2} = 0\]
From (ii), we get,
\[{x_2} + {x_3} = 0\]
\[{y_2} + {y_3} = 2\beta \]
\[{z_2} + {z_3} = 0\]
From (iii), we get,
\[{x_3} + {x_1} = 0\]
\[{y_3} + {y_1} = 0\]
\[{z_3} + {z_1} = 2\gamma \]
From all the above equations, we can conclude that,
\[{x_1} + {x_2} + {x_3} = \alpha \]
\[{y_1} + {y_2} + {y_3} = \beta \]
\[{z_1} + {z_2} + {z_3} = \gamma \]
Hence, we get the coordinates of the points A,B,C in terms of \[\alpha ,\beta ,\gamma \]
Step 2: We will now find out the coordinate of centroid of the triangle coordinate of the centroid of the triangle is given by
\[(\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3})\]
= \[(\dfrac{\alpha }{3},\dfrac{\beta }{3},\dfrac{\gamma }{3})\]
Hence, the coordinate of the centroid of the triangle ABC is \[(\dfrac{\alpha }{3},\dfrac{\beta }{3},\dfrac{\gamma }{3})\].
So, \[D(\dfrac{\alpha }{3},\dfrac{\beta }{3},\dfrac{\gamma }{3})\] is the correct answer.

Note: Diagram should be drawn properly. As because, a correct diagram will only lead you to a correct answer. Also, equations should be written correctly.