Question

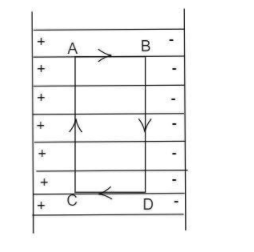
A uniform electric field $E$ exists between two charged plates. What would be the work done in moving a charge $q$ along the closed $ABCDA$ ?

(A) $\oint {E.dl} $
(B) $ - \oint {E.dl} $
(C) Zero
(D) None of these

Answer 1

Hint:Consider the charge at any point and it is moved along the closed rectangle $ABCDA$ . Find the work done to move a charge from that point to reach the point again in a closed loop by using the formula of the work done given below.

Useful formula:
The formula for the work done to move the charge along the electric field is given by
$w = \int {\vec E.d\vec l} $
Where $w$ is the work done, $\vec E$ is the electric field along with its direction and $dl$ is the change in the length.

Complete step by step solution:
The electric field lines in the given diagram, shows that it moves from the positive charge and reaches the negative charge. Let us consider that the charge $q$ is placed at the point $A$ , then the work is done to move the charge along the closed lines $ABCDA$ .
$w = \int {\vec E.d\vec l} $
Since $\vec E$ is constant,
$w = \vec E\int {d\vec l} $
Since the length remains the same, the change in the length tends to zero. Hence,
$w = \vec E\int {\vec 0} $
The integration of the zero is also zero, substituting that in the above equation, we get
$w = 0$
Hence the work done to bring the charge $q$ along the closed line $ABCDE$ is zero.

Thus the option (C) is correct.

Note:The work done in bringing the charge along the closed path is always zero. This is because the closed path has a uniform electric field in its entire area and the electrostatic forces in it is conservative forces and hence the value of the work done is zero.