Question

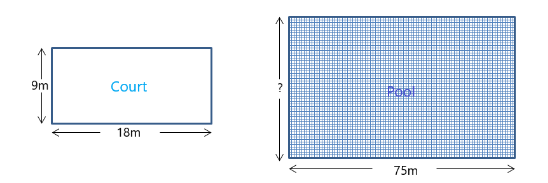
A volleyball court is in a rectangular shape and its dimensions are directly proportional to the dimensions of the swimming pool given below. Find the width of the pool.

Answer 1

Hint: If two amounts change at the same rate, they are said to be proportional. There are many definitions of proportionality but the simplest one is that if two ratios are equal then they are proportional. We have to use this definition of proportionality to get the correct answer to the above question.

Complete step-by-step answer:
From the figure, we can see that the length of the court is 18m and its breadth is 9m, and the length of the pool is 75m while its width is not known to us. Let the width/breadth of the court be x.
Two things are proportional if their ratio is the same or constant or they have the same relative size.
Now, we know that the dimensions of the court are proportional. So,
 $ \dfrac{{length\,of\,court}}{{breadth\,of\,court}} = \dfrac{{length\,of\,pool}}{{breadth\,of\,pool}} $
Putting the required values in the above equation, we get –
 $
\Rightarrow \dfrac{{18m}}{{9m}} = \dfrac{{75m}}{x} \\
\Rightarrow 2 = \dfrac{{75}}{x} \\
\Rightarrow x = \dfrac{{75}}{2} = 37.5m \;
  $
Hence, the width of the court is 37.5m
So, the correct answer is “37.5 m”.

Note: There are two types of proportionality:
Directly proportional – When one quantity increases, the other quantity also increases at the same rate, the two quantities are said to be directly proportional.
Inversely proportional – when one quantity increases, the other quantity decreases at the same rate, the two quantities are said to be inversely proportional.
In this question, the dimensions are proportional, that is the dimensions of both quantities have the same ratio. Make sure that all the dimensions should have the same S.I. units.