Question

A well of diameter 14 m, is drug 15 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 7 m to take an embankment. Find the height of the embankment.

Answer 1

Hint: Here, we will find the radius \[r\] of the given well from the given value of diameter of a well and then use formula of the volume of mud is \[\pi {r^2}h\], where \[r\] is the radius and \[h\] is the height of the cylinder. Then we will find the area of the ring using the formula of area of circle, \[\pi {r^2}\], where \[r\] is radius of circle in both the circle by subtracting the area of well from the area of embankment. Then we will compute the height of the embankment can be calculated by dividing the volume of mud by area of ring, that is, \[{\text{Height}} = \dfrac{{{\text{Volume of mud}}}}{{{\text{Area of ring}}}}\].

Complete step-by-step answer:
We are given that the diameter \[d\] of a well is 14 m and the height of a well is 15 m.
We will now find the radius \[r\] of the given well from the above value of diameter of a well.
\[
   \Rightarrow r = \dfrac{{14}}{2}{\text{ m}} \\
   \Rightarrow r = 7{\text{ m}} \\
 \]
We know that the formula of the volume of mud is \[\pi {r^2}h\], where \[r\] is the radius and \[h\] is the height of the cylinder.
Substituting the values of \[r\] and \[h\] in the above formula of volume of a well, we get
\[
   \Rightarrow {\text{Volume of mud = }}\dfrac{{22}}{7} \times {7^2} \times 15 \\
   \Rightarrow {\text{Volume of mud }} = 22 \times 7 \times 15 \\
   \Rightarrow {\text{Volume of mud }} = 2310{\text{ }}{{\text{m}}^3} \\
 \]
Thus, the volume of mud is \[2310{\text{ }}{{\text{m}}^3}\].
We are given that the shape of a circular ring of width 7 m is taken to an embankment in a well.

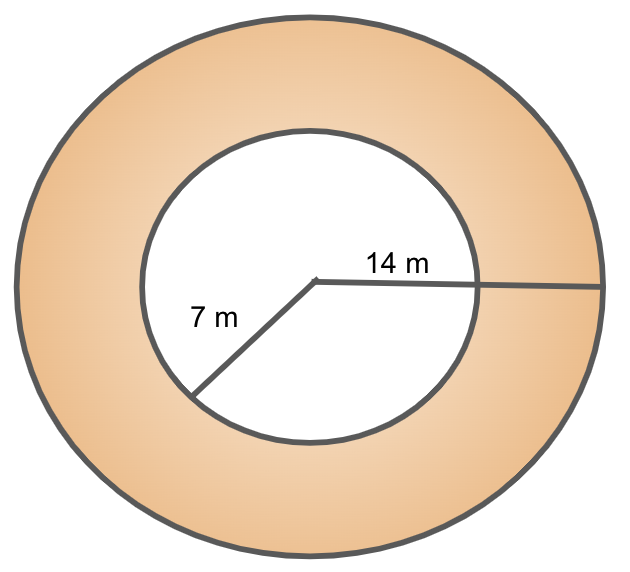
We will now find the area of the shaded region to find the area of ring using the formula of area of circle, \[\pi {r^2}\], where \[r\] is radius of circle in both the circle, we get
\[
  {\text{Area of ring}} = \pi {\left( {14} \right)^2} - \pi {\left( 7 \right)^2} \\
   = 196\pi - 49\pi \\
   = 147\pi \\
 \]
Substituting the value of in the above equation, we get
\[
   \Rightarrow {\text{Area of ring}} = 147 \times \dfrac{{22}}{7} \\
   \Rightarrow {\text{Area of ring}} = 462{\text{ }}{{\text{m}}^2} \\
 \]
Thus, the area of the ring is \[147\pi {\text{ }}{{\text{m}}^2}\].
We know that the height of the embankment can be calculated by dividing the volume of mud by area of ring, that is, \[{\text{Height}} = \dfrac{{{\text{Volume of mud}}}}{{{\text{Area of ring}}}}\].
Substituting the values of volume of mud and area of ring in the above formula of height, we get
\[
   \Rightarrow {\text{Height}} = \dfrac{{2310}}{{462}} \\
   \Rightarrow {\text{Height}} = 5{\text{ m}} \\
 \]
Hence, the height of an embankment is 5 m.

Note: While solving these types of questions, you should be familiar with the formulas of volume of cylinder and area of circle. Students should read the question carefully and then make the diagram for better understanding. We have to use the formula for the height of the embankment, which is calculated by dividing the volume of mud by area of ring, that is, \[{\text{Height}} = \dfrac{{{\text{Volume of mud}}}}{{{\text{Area of ring}}}}\] to find the right answer.