Question

(A) What characteristic property of nuclear force explains the constancy of binding energy per nucleon (BE/A) in the range of mass number ‘A’ lying 30(B) Show that the density of the nucleus over a wide range of nuclei is constant-independent of mass number A.

Answer 1

Hint: Binding energy is the energy required to separate the nucleons from each other in the nucleus of the atom. The mass of the nucleus formed by the combination of the nucleons like protons and neutrons is slightly lesser than the sum of individual masses of the nucleons. This difference in mass is called mass defect. If one wonders why there is a decrease in mass, it is because when the nucleons are bound, they lose some energy to bind to each other. This lost energy corresponds to the decrease in mass accounted for, due to Einstein's mass-energy equation.
Einstein’s mass energy relation: $E = m{c^2}$ - where c is the speed of light in vacuum.
Mass-defect, $\Delta M = \left[ {Z{m_p} + \left( {A - Z} \right){m_n}} \right] - M$
where, M= mass of nucleus, Z = atomic number, A= mass number, ${m_p}\& {m_n}$are masses of proton and neutron respectively,
Binding energy,
 $
  BE = \Delta M.{c^2} \\
  Substituting, \\
  BE = \left[ {\left( {Z{m_p} + \left( {A - Z} \right){m_n}} \right) - M} \right].{c^2} \\
 $
Complete step by step answer:
(A) The binding energy per nucleon is obtained by dividing the binding energy by the mass number. The binding energy per nucleon is a denotation of the stability of a nucleus. Here is the graph of binding energy per nucleon to the mass number:

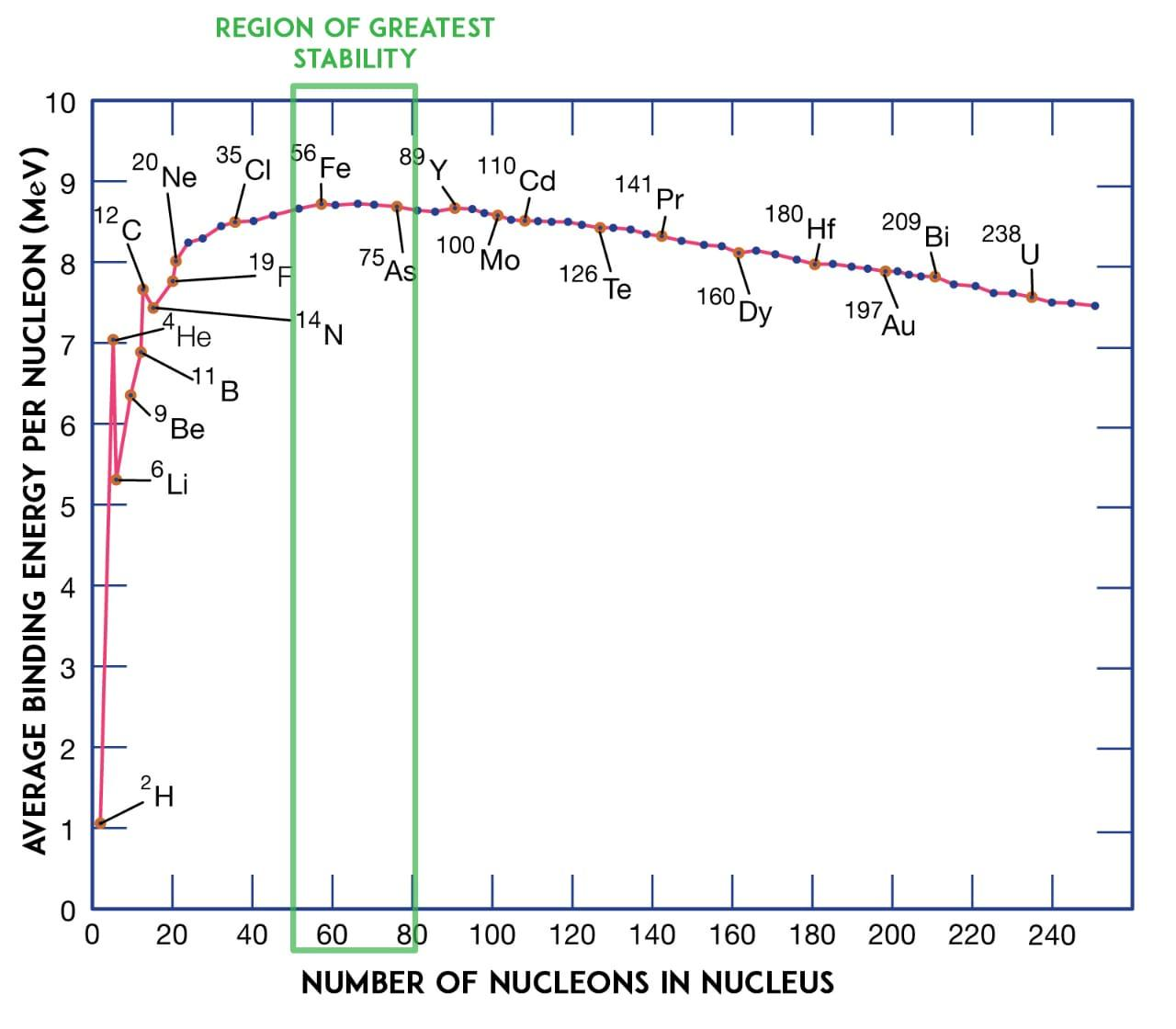
As you can see from the above graph, the average binding energy per nucleon is almost constant for the mass numbers ranging from $30 < A < 170$.
The characteristic property attributed to the constant average binding energy per nucleon for atoms under $30 < A < 170$ is that the nuclear energy is short-range force.
The reason is explained as here:
Nuclear energy is a short-ranged force, which means that the nucleon will only exert its nuclear force over a short range around itself. This effect can only be felt on a fixed number of nucleons around its vicinity in the nucleus, unlike electrostatic force whose magnitude varies as there are a greater number of charges in its vicinity.
Thus, even if we add a few nucleons by increasing the A, the nuclear force will not alter considerably, since the area of influence by the nucleon is fixed. With the nuclear force being constant, the average binding energy per nucleon will not change considerably over the range of mass numbers from 30-170.

(B) The density of the nucleus is independent of the mass number over a wide range of atoms. This can be explained in the following way:
The nucleus of mass number A has the radius equal to –
$R = {R_0}\sqrt[3]{A}$
The value of ${R_0} = 1.2 \times {10^{ - 15}}m$
Assuming that the nucleus is a sphere, the volume of the nucleus is –
\[
  V = \dfrac{4}{3}\pi {R^3} \\
  Substituting, \\
  V = \dfrac{4}{3}\pi {\left( {{R_0}\sqrt[3]{A}} \right)^3} \\
  Solving, \\
  V = \dfrac{4}{3}\pi \left( {{{\left( {{R_0}} \right)}^3}{{\left( {\sqrt[3]{A}} \right)}^3}} \right) \\
  V = \dfrac{4}{3}\pi A{R_0}^3 \\
 \]
Mass of the nucleus –
$M = A({m_p} + {m_n})$
where A – mass number and ${m_p}\& {m_n}$are mass of proton and neutron respectively,
$
  Density, \\
  \rho = \dfrac{M}{V} \\
  Substituting, \\
  \rho = \dfrac{{{A}({m_p} + {m_n})}}{{\dfrac{4}{3}\pi {A}{R_0}^3}} \\
  \rho = \dfrac{{{m_p} + {m_n}}}{{\dfrac{4}{3}\pi {R_0}^3}} \\
 $
Since, in this equation, all the values such as ${R_0},{m_p}\& {m_n}$ are fixed values, the value of nuclear density is a constant number and it is independent of the mass number A.

Note: The approximate value of nuclear density is $2.3 \times {10^{17}}kg{m^{ - 3}}$. This exceptionally high value of the nuclear density tells us that all the nucleons are closely packed together and supports the theory that the atom has a large amount of empty space, almost nearly empty.