Question

A wheel and axle having total moment of inertia of $2\times {10}^{-3}kg{m}^2$ is made to rotate about its own axis by means of 1 kg attached to a cord wrapped around the axle. The axle has a radius of 1cm. How far must the weight descent approximately so that the flywheel acquires the speed of 31.4 rad/sec?

Answer 1

Hint:When a mass is tied around the axle, it pulls down the cord thereby, rotating the axle. Here, the total energy of the system is conserved i.e. the gain in potential energy by the mass when it is pulled down is equal to the loss in kinetic energy of the rotating axle.

Complete step-by-step answer:
Consider a flywheel-axle setup with a weight of 1kg hanging downwards as shown:

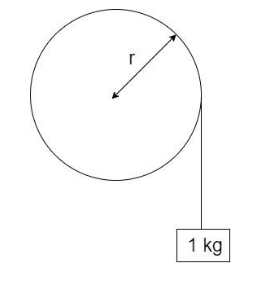
Because of the weight acting, the block goes further downwards to a height of h, the rotational speed of flywheel is restricted to 31.4 radians per second, as shown:

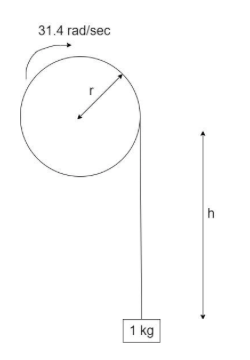
Since the block moves to a height of h, it gains potential energy. This gain in potential energy is at the expense of the loss in kinetic energy of rotation of the flywheel, since the total energy of the system is always conserved.
Hence,
Gain in PE = Loss of KE
Gain in potential energy of the block = $mgh$ where m = mass of the block and g = acceleration due to gravity.
Loss of kinetic energy is equal to the sum of kinetic energy due to linear velocity and kinetic energy due to inertial effect of the flywheel.
Kinetic energy due to linear velocity, v – ${\displaystyle \frac{1}{2}}m{v}^2$
Kinetic energy due to inertia – ${\displaystyle \frac{1}{2}}I{\omega }^2$
where I – inertia and $\omega$ - angular velocity.
Loss of kinetic energy = ${\displaystyle \frac{1}{2}}m{v}^2+{\displaystyle \frac{1}{2}}I{\omega }^2$
The linear velocity of rotation, v is the product of radius and the angular velocity.
$v=r\omega$
Substituting, we get –
KE = ${\displaystyle \frac{1}{2}}m{r}^2{\omega }^2+{\displaystyle \frac{1}{2}}I{\omega }^2$
By conservation of energy, we have –
$mgh={\displaystyle \frac{1}{2}}m{r}^2{\omega }^2+{\displaystyle \frac{1}{2}}I{\omega }^2$
Given,
Mass of the block, m = 1 kg Radius, r = 1 cm = 0.01m Acceleration due to gravity, $g=9\cdot 81m{s}^{-2}$ Moment of inertia, $I=2\times {10}^{-3}kg{m}^2$ Angular velocity, $\omega =31\cdot 4rad{s}^{-1}$
Substituting these values,
$mgh={\displaystyle \frac{1}{2}}m{r}^2{\omega }^2+{\displaystyle \frac{1}{2}}I{\omega }^2$
$1\times 9\cdot 81\times h={\displaystyle \frac{1}{2}}\times 1\times 0\cdot {01}^2\times 31\cdot 4^2+{\displaystyle \frac{1}{2}}\times 2\times {10}^{-3}\times 31\cdot 4^2$
Solving,
$1\times 9\cdot 81\times h=0\cdot 049+0\cdot 985$
$\therefore h={\displaystyle \frac{1\cdot 034}{9\cdot 81}}=0\cdot 105m$
Therefore, the height of descent of the block is to be, h = 0.105 m

Note:One of the most common applications of flywheel is the areas where we need to smoothen out the power output of an energy source, that produces energy in pulses or regular intervals, such as internal combustion engines in the automobiles. Along with the function of smoothing out the power, the flywheel, additionally, acts as surge protector. This means that when the power output in the engine fluctuates suddenly, the jerk is not felt at the output because the flywheel absorbs the surge power and smooths it out.