Question

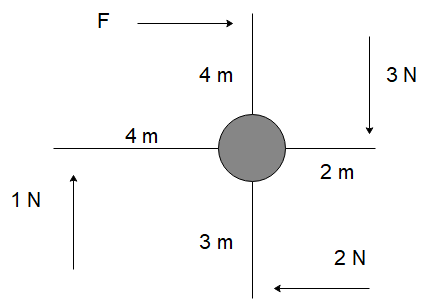
A windmill is pushed by four external forces as shown. Calculate the force $ F $ required to make the windmill standstill.

A) 2 N
B) -4 N
C) 6 N
D) -16 N

Answer 1

Hint: In this solution, we will calculate the torque generated by each of the four external forces. The force $ F $ should be such that the net torque will be zero.

Formula used In this solution, we will use the following formula:
- Torque due to a force: $ \tau = F \times r $ where $ F $ is the external force and $ r $ is the distance where the force is acting from the axis of rotation.

Complete step by step answer:
As we can see in the figure, the windmill is being acted on by four different forces. The force $ F $ should be such that the net torque due to all these forces should add up to zero.
WE know that the torque due to an external force is calculated as $ \tau = F \times r $ . Here $ r $ is the distance of the point where the force is acting with the axis of rotation. In the figure, we can see that all the forces are acting on the edges of the sides of the windmill. Also, as the length of the edges of the windmill are perpendicular to the direction of the force, we can calculate the net torque on the system as
 $ \tau = \left( {3 \times 2} \right) + \left( {F \times 4} \right) + \left( {2 \times 3} \right) + \left( {1 \times 4} \right) $
To make the windmill standstill, the net torque on it must be still. Hence, we can write
 $ 0 = \left( {3 \times 2} \right) + \left( {F \times 4} \right) + \left( {2 \times 3} \right) + \left( {1 \times 4} \right) $
Then we can solve for $ F $ as
 $ 4F = - 16 $
Or
$ F = - 4\,N $ which corresponds to option (B).

Note:
Since the windmill is an object that has rotational motion, we must know that for it to be stationary, the net torque on it has to be zero and not the net force. Also, we must take into account the direction of force acting on the windmill. Since the value of $ F $ is negative, it means the direction of force is opposite to that shown in the question. This is the only way the windmill can stay stationary since all other forces support each other.