Question

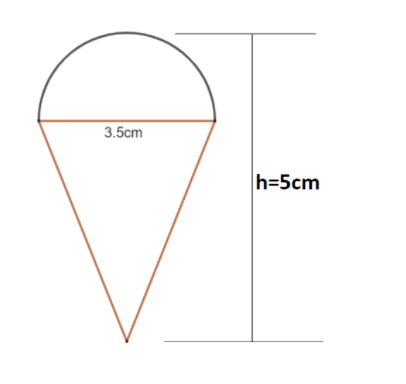
A wooden Lattu’s top is shaped like a cone surrounded by a hemisphere as shown in the figure. The total height of the top is 5cm and the diameter of the top is 3.5cm. A boy wants to color it. Find the area he will have to color.

Answer 1

Hint: This problem is a combination of two shapes that are cone and hemisphere. So we will find the area of both the shapes. Sometimes we need to calculate the dimensions of the shapes from the given data. So we will calculate the height of the cone and that of the hemisphere separately. On adding their areas we will get the area of the top and so the area to be colored by the boy.

Complete step by step solution:
Given is the wooden top made up of a cone with a hemisphere above it.
Area of hemisphere:
We know that area of the hemisphere is given by the formula \[2\pi {r^2}\].
But we have no idea of the radius of the hemisphere. But from the figure we can see that the diameter of the cone is the diameter of the hemisphere. So from that we can calculate the radius.
So, \[{r_{hemisphere}} = \dfrac{d}{2}\]
Now the diameter is 3.5cm
\[{r_{hemisphere}} = \dfrac{{3.5}}{2}\]
On dividing we get,
\[{r_{hemisphere}} = 1.75cm\]
This is the radius. Now we will calculate the area.
\[{A_{hemisphere}} = 2\pi {r^2}\]
Putting the values we get,
\[ = 2 \times 3.14 \times {\left( {1.75} \right)^2}\]
On calculating we get,
\[{A_{hemisphere}} = 19.2325c{m^2}\]
Thus this is an area of one part.
Area of cone:
We know that area of the cone is given by \[\pi rl\] .
But the height is mentioned from top to bottom that includes that of the hemisphere also. So to get the length or height of the cone only we will remove the height of the hemisphere from the total height.
\[{h_{cone}} = 5 - {r_{hemisphere}}\]
Radius of the hemisphere is its height here.
\[{h_{cone}} = 5 - 1.75\]
On subtracting we get,
\[{h_{cone}} = 3.25cm\]
Thus this is the height.
Now we will calculate the area,
\[{A_{cone}} = \pi rh\]
Putting the values,
\[{A_{cone}} = 3.14 \times 1.75 \times 3.25\]
On multiplying we get,
\[{A_{cone}} = 17.8587c{m^2}\]
This is the area of the second part also.
Now to get the area of the total top we will add them.
\[{A_{top}} = {A_{hemisphere}} + {A_{cone}}\]
Putting the values,
\[{A_{top}} = 19.2325c{m^2} + 17.8587c{m^2}\]
On adding we get,
\[{A_{top}} = 37.0912c{m^2}\]
This is the area that boy has to color. Or to get more précised,
\[{A_{top}} \simeq 37.1c{m^2}\]
This will be more correct.
Boy will color \[{A_{top}} \simeq 37.1c{m^2}\] area.
So, the correct answer is “\[{A_{top}} \simeq 37.1c{m^2}\] ”.

Note: Note that the top part of cone and lower part of hemisphere is same. And they are stuck to each other. So we have not calculated that area and not even considered it. Also note that when we take lateral surface area and when we take total surface area is important.