Question

A wooden toy rocket in the shape of a cone mounted on a cylinder, as shown in the figure. The height of the entire rocket is 26cm. While the height of the conical part is 6cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylinder portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colors, (take ($\pi = 3.14$)).

Answer 1

Hint: In this particular question use the concept that yellow part of the rocket = curved surface area of the cylinder + base of the cylinder (which is in circular shape only the lower base is considered as the upper base of the cylinder is not included in paint) and the orange part of the rocket = curved surface area of the cone + surface area of the base (only portion which is painted orange) so use these concepts to reach the solution of the question.

Complete step-by-step answer:

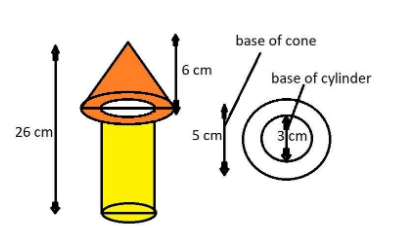
Height of the entire rocket, H = 26 cm.
Height of the cone, h = 6 cm.
Diameter of the base of the cone, D = 5 cm.
Diameter of the base of the cylinder, d = 3 cm.
Now as we know that the radius is half of the diameter.
So the radius of the cone, $R = \dfrac{D}{2} = \dfrac{5}{2}$ cm
And the radius of the cylinder, $r = \dfrac{d}{2} = \dfrac{3}{2}$ cm
So the height of the cylinder = height of the entire rocket – height of the cone.
So the height of the cylinder, h’ = 26 – 6 = 20 cm.
Now we have to paint yellow to the cylindrical part of the rocket and orange to the cone part of the rocket as shown in the figure.
We have to find the area of the rocket painted with each of these colors.
So, the yellow part of the rocket = curved surface area of the cylinder + base of the cylinder (which is in circular shape only the lower base is considered as the upper base of the cylinder is not included in paint as shown in the figure).
Curved surface area of the cylinder = $2\pi rh'$.
Base of the cylinder (which is in circular shape) = $\pi {r^2}$.
So, the yellow part of the rocket = $2\pi rh'$ + $\pi {r^2}$ square units.
Where, r and h’ are the radius and the height of the cylinder.
 Now substitute the values in the above equation we have,
So, yellow part of the rocket = $2\left( {3.14} \right)\left( {\dfrac{3}{2}} \right)\left( {20} \right) + 3.14{\left( {\dfrac{3}{2}} \right)^2}$ square cm.
Now simplify this we have,
So, the yellow part of the rocket = $188.57 + 7.07 = 195.64$ square cm.
Now the orange part of the rocket = curved surface area of the cone + surface area of the base (only portion which is painted orange).
Curved surface area of the cone = $\pi RL$
Surface area of the base (only portion which is painted orange) = $\pi {\left( {R - r} \right)^2}$
Where, R, r and L are the radius of the cone, radius of the cylinder and the slant height of the cone respectively.
So, the orange part of the rocket = $\pi RL + \pi {\left( {R - r} \right)^2}$
Now the slant height of the cone is given as, $L = \sqrt {{h^2} + {R^2}} $, where (h) is the height of the cone.
So, the orange part of the rocket = $\pi R\left( {\sqrt {{h^2} + {R^2}} } \right) + \pi \left( {{R^2} - {r^2}} \right)$ square cm.
Now substitute the values we have,
So, the orange part of the rocket = $3.14\left( {\dfrac{5}{2}} \right)\left( {\sqrt {{6^2} + {{\left( {\dfrac{5}{2}} \right)}^2}} } \right) + 3.14\left( {{{\left( {\dfrac{5}{2}} \right)}^2} - {{\left( {\dfrac{3}{2}} \right)}^2}} \right)$ square cm.
Now simplify this we have,
So, the orange part of the rocket = $51.025 + 12.56 = 63.585$ square cm.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall all the formulas of the cylinder as well as cone which is all stated above, then first calculate the area of the portion which is painted yellow then area of the portion which is painted orange as above which is the required answer.