Question

A yo-yo has mass$\;m$, inner radius$\;r$ and outer radius$\;R$. Its moment of inertia is$\;I$ about its centre. The yo-yo rolls without slipping on a horizontal table, and is pulled along by a horizontal string wound around its inner radius. The pulling by the string with tension$\;T$ gives rise to an acceleration$\;a$. The yo-yo rolls without slipping. What is the magnitude of acceleration$\;a$?
A. $\dfrac{TR(R-r)}{1+mR^2}$
B. $\dfrac{TR(R+r)}{1-mR^2}$
C. $\dfrac{TR(2r+R)}{1+mR^2}$
D. None of these

Answer 1

Hint: Begin by deducing the equations for equilibrium of forces in the horizontal and vertical directions. Be sure to account for the frictional force encountered by the yo-yo as it is pulled by the string. Plug in the frictional force expression into one of the force equilibrium equations and keep in mind to distinguish the radial and tangential quantities introduced in the equations. Rearrange the resulting equations and evaluate them to arrive at an expression for the acceleration accordingly.

Formula used: Torque $\tau = I\alpha$
Gravitational force: $F_g =mg$
Accelerative force: $F_{a} = ma$

Complete step by step answer:
We are given that the mass of the yo-yo is$\;m$, and its inner radius is$\;r$ and outer radius is$\;R$. The yo-yo is said to roll without slipping on a horizontal table.
Let the acceleration with which the yo-yo rolls be $\alpha$. Given that the moment of inertia of the yo-yo about its centre is$\;I$, the torque acting on the yo-yo will be:
$\tau = I\alpha$

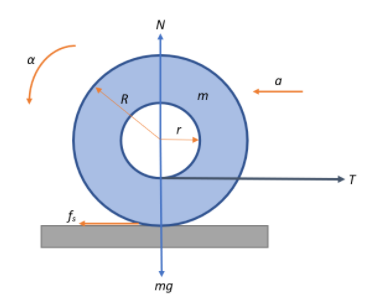
The gravitational force acting on the yo-yo is $F_{g} = mg$, in response to which it experiences a normal force$\;N$.
As the string is pulled, the yo-yo experiences a linear accelerative force $F_a = ma$
Now, let us look at the equilibrium of forces about the x and y-directions as the yo-yo is pulled along by a string with tension$\;T$, under the influence of a frictional force $f_s$ as a result.
Along the horizontal direction or the x-axis, we have:
$T-f_s = F_a \Rightarrow T -f_s = ma$
Along the vertical direction or the y-axis, we have:
$N-mg = 0$
Along the radial direction:
We know that due to the pulling of the string which is responsible for producing a torque that makes the yo-yo roll, the yo-yo radially experiences tension along its inner radius and a frictional force about its outer radius, i.e.,
$\tau = Rf_s-rT$
But we know that $\tau =I\alpha$
So, we get:
$I\alpha = Rf_{s}-rT$
But, we know that $\alpha = \dfrac{a}{R}$, so plugging this back into our equation we get:
$\dfrac{Ia}{R} = Rf_s-rT$
Re-arranging this equation for $f_s$, we get:
$Rf_{s} = rT + \dfrac{Ia}{R}$
$\Rightarrow f_{s} = \dfrac{rT}{R} + \dfrac{Ia}{R^2}$
Substitute the above expression for $f_s$ in the horizontal force equilibrium equation, we get:
$T -f_{s} = ma$
$\Rightarrow T - \left(\dfrac{rT}{R} + \dfrac{Ia}{R^2}\right) = ma$
$\Rightarrow T - \dfrac{rT}{R} - \dfrac{Ia}{R^2} = ma$
$\Rightarrow ma + \dfrac{Ia}{R^2} = T - \dfrac{rT}{R}$
$\Rightarrow a\left(m+\dfrac{I}{R^2}\right) = T\left(1 - \dfrac{r}{R}\right)$
$\Rightarrow a\left(\dfrac{mR^2+I}{R^2}\right) = T\left(\dfrac{R - r}{R}\right)$
$\Rightarrow a\left(\dfrac{mR^2+I}{R}\right) = T\left(R - r\right)$
$\Rightarrow a = \dfrac{TR(R-r)}{mR^2+I} = \dfrac{TR(R-r)}{I+mR^2}$

So, the correct answer is “Option A”.

Note: It is important to understand the distinction between linear acceleration (a) and angular acceleration ($\alpha$) and establish a relationship between the two. Linear acceleration is generally associated with linear displacements or linear motion which is any motion that occurs along a straight line in one direction, whereas angular acceleration is associated with angular displacements or rotatory motion which is any motion where a body moves in a circular path about an axis of rotation.
Linear acceleration $a = r\alpha$, where r is the radius of the circular path traced.
Note that though linear acceleration is associated with straight line motion, it is also a measurable quantity in circular motion in addition to the angular acceleration. The linear acceleration at a point is directed tangentially away from the radius of the path and is called the tangential acceleration, whereas the angular acceleration is directed radially and is appropriately called the radial acceleration.