Question

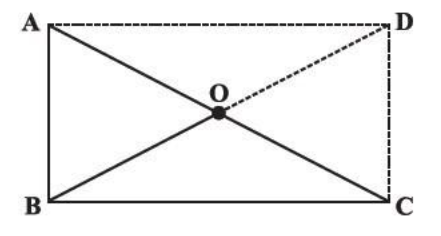
ABC is a right-angled triangle and O is the midpoint of the side opposite to the right angle. Explain why O is equidistant from A, B and C.
(The dotted lines are drawn additionally to help you)

Answer 1

Hint: First we will draw a line from A parallel to BC and a line from C parallel to BA. Then we will let them meet at point D and join OD. Then we will prove ABCD is parallelogram as opposite sides are parallel and then prove this parallelogram to be a rectangle by using the basic properties of a rectangle. We will use the property of a rectangle that the diagonal of a rectangle bisect other and are of equal length to prove.

Complete step by step solution: We are given that ABC is a right-angled triangle and O is the midpoint of the side opposite to the right angle.

First, we will draw a line from A parallel to BC and a line from C parallel to BA.
Then we will let them meet at point D and join OD.

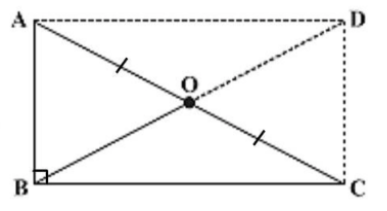
First, we will take ABCD, where we know that \[{\text{AB||DC}}\] and \[{\text{BC||AD}}\] by our above construction.
Thus, the opposite sides are parallel.
Hence, ABCD is a parallelogram.

We also know that adjacent angles of a parallelogram are supplementary, from the above diagram, the sum of angle \[\angle ABC\] and \[\angle BCD\] is \[180^\circ \], we have
\[ \Rightarrow \angle ABC + \angle BCD = 180^\circ \]

Substituting the value of \[\angle ABC\] in the above equation, we get
\[ \Rightarrow 90^\circ + \angle BCD = 180^\circ \]

Subtracting both sides by \[90^\circ \] in the above equation, we get
\[
   \Rightarrow 90^\circ + \angle BCD - 90^\circ = 180^\circ - 90^\circ \\
   \Rightarrow \angle BCD = 90^\circ \\
 \]

Also, we know that the opposite angles of a parallelogram are equal, so we have
\[
   \Rightarrow \angle DAB = \angle BCD \\
   \Rightarrow \angle DAB = 90^\circ \\
 \]

\[
   \Rightarrow \angle ADC = \angle ABC \\
   \Rightarrow \angle ADC = 90^\circ \\
 \]

Therefore, each angle of the parallelogram ABCD is a right angle.

So we know that when a parallelogram with all right angles is a rectangle.

Thus, ABCD is a rectangle.

We also know that the diagonals of a rectangle bisect each other, then we have from the above diagram that
\[ \Rightarrow OA = OC = \dfrac{1}{2}AC{\text{ ......eq.(1)}}\]
\[ \Rightarrow OB = OD = \dfrac{1}{2}BD{\text{ ......eq.(2)}}\]

We also know that the diagonal of a rectangle are equal length, then we have
\[ \Rightarrow BD = AC\]

Dividing both sides by 2 in the above equation, we get
\[ \Rightarrow \dfrac{1}{2}BD = \dfrac{1}{2}AC\]

Using equation (1) and equation (2) in the above equation, we get
\[ \Rightarrow OB = OA\]

Therefore, we have found out that \[OB = OA = OC\].
Hence, O is equidistant from A, B and C.
Hence, proved.

Note: In solving these types of questions, you need to know that the properties of rectangles and their diagonals. Then we will use the properties accordingly. This is a simple problem, one should only need to know the definitions. It is clear from the diagram that it is a rectangle as nowhere it is given it to be a square, so remember that as well.