Question

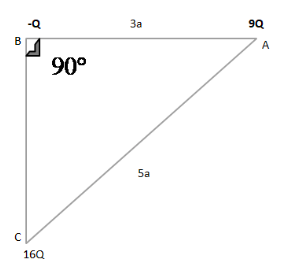
ABC is a right-angled triangle. Calculate the magnitude of the force on a charge –Q.
     

Answer 1

Hint:Here, we use the concept of Coulomb's law, which states that the force of attraction or repulsion between any two charged bodies is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.

Formula used:
${\rm{F}}\; = \;{\dfrac{1}{{4\pi \in }}_o}\;\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
F is force, q1, and q2 are charged, and r is the square of the distance between them and ${ \in _o}$ is absolute permittivity.

Complete step by step answer:
According to the given diagram, first, we find the distance of BC by using Pythagoras theorem:
${{\rm{(AC)}}^2} = \;{({\rm{BA)}}^2}\; + \;{({\rm{BC)}}^2}$
The given value of AC = 5a, BA = 4a
${({\rm{BC)}}^2} = \;{(5a{\rm{)}}^2} - \;{(3a)^2}$
${({\rm{BC)}}^2}\; = \;25{a^2} - \;9{a^2}$
${\rm{B}}{{\rm{C}}^2} = 16{a^2}$
${\rm{BC}}\; = 4a$
Now, the force due to the charge at A is given by the above formula,
${{\rm{F}}_1}\; = \;{\dfrac{1}{{4\pi \in }}_o} \times \;\dfrac{{\left( { - {\rm{Q}}} \right) \times \left( {9{\rm{Q}}} \right)}}{{9{a^2}}}\; = \,{\dfrac{1}{{4\pi \in }}_o} \times \;\dfrac{{\left( { - {{\rm{Q}}^2}} \right)}}{{{a^2}}}$
Force on charge C is given as,
${{\rm{F}}_2}\; = \;{\dfrac{1}{{4\pi \in }}_o} \times \;\dfrac{{\left( { - {\rm{Q}}} \right) \times \left( {{\rm{16Q}}} \right)}}{{16{a^2}}}\; = \,{\dfrac{1}{{4\pi \in }}_o} \times \;\dfrac{{\left( { - {{\rm{Q}}^2}} \right)}}{{{a^2}}}$
Therefore total net force is given as,
$\left| {{{\rm{F}}_{net}}} \right|\; = \;\sqrt {{{\rm{F}}_1} + {{\rm{F}}_2}} $
$ \Rightarrow \;{{\rm{F}}_{net}}\; = \;\dfrac{1}{{4\pi { \in _o}}} \times \sqrt 2 \dfrac{{{{\rm{Q}}^2}}}{{{{\rm{a}}^2}}}$
$ \Rightarrow \;\;{{\rm{F}}_{net}}\; = \;\dfrac{{\sqrt 2 }}{{4\pi { \in _o}}} \times \dfrac{{{{\rm{Q}}^2}}}{{{r^2}}}$
Thus, the magnitude of the force on a charge –Q is $\dfrac{{\sqrt 2 }}{{4\pi { \in _o}}} \times \dfrac{{{{\rm{Q}}^2}}}{{{r^2}}}$

Note:The "Coulomb's law applies to only stationary electric charges" because, in case of moving charges, there is a current, which generates a magnetic field that, in turn, exerts a force on moving charges. Therefore we no longer consider Coulomb's Force alone. Also it signifies the inverse square dependence of electric force. It can also be used to obtain simple derivations of Gauss' law for general cases accurately. The vector form of Coulomb's law is important as it helps us specify electric fields' direction due to charges. It is also written as its abbreviation 'C,' is the SI unit for electric charge. One Coulomb is defined as the amount of charge from a current of one ampere flowing for one second. The charge of an electron is $1.6 \times {10^{ - 19}}$C.