Question

ABCD is a parallelogram M is the midpoint of DC. If AP=65 and PM=30, then the largest possible integer value of AB is

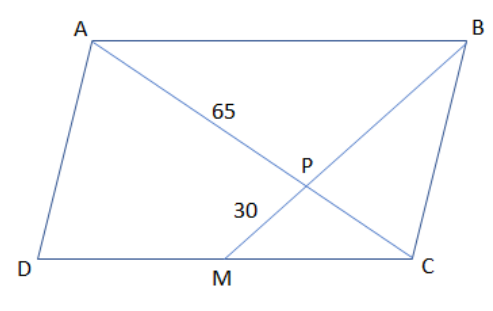
(a) 124
(b) 120
(c) 119
(d) 118

Answer 1

Hint: First, here we use the condition of the similarity of the triangles. Then, by using the condition of the similarity that the ratio of the sides of the similar triangles is always equal. Then, by using the condition that the sum of two sides of the triangle is always greater than the third side, we get the final result.

Complete step-by-step solution:
In this question, we are supposed to find the largest possible integral value of AB from the parallelogram ABCD drawn with conditions as:

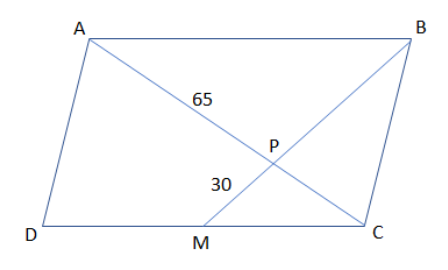
Now, we have drawn the conditions from the question in the figure that PM=30 and AP=65.
Then, here we use the condition of that the triangles between the parallel lines AB and CD give the two triangles CMP and triangle ABP as similar by using the following property.
Now, we can also prove that by using the given figure with the condition that lines DC and AB are parallel in two triangle CMP and triangle ABP which gives:
$\angle APB=\angle CPM$ (vertically opposite angle)
$\angle PAB=\angle PCM$ (alternate interior angle)
$\angle PBA=\angle PMC$ (alternate interior angle)
So, by using the AAA property, we can conclude that $\Delta ABP\sim \Delta CMP$.
Now, by using the condition of the similarity that the ratio of the sides of the similar triangles is always equal.
So, by using the above-stated property and the condition is given in the question that M is the midpoint on DC, we get:
$\dfrac{AB}{MC}=\dfrac{BP}{MP}=\dfrac{AP}{CP}=\dfrac{2}{1}$
So, by using one of the ratios of the above condition, we know the value of the side PM=30.
Then, by using the ratio as:
$\dfrac{BP}{MP}=\dfrac{2}{1}$
Now, by substituting the value of PM=30 as:
$\begin{align}
  & BP=2\times MP \\
 & \Rightarrow BP=2\times 30 \\
 & \Rightarrow BP=60 \\
\end{align}$
Then, by using the condition that the sum of two sides of triangle is always greater than the third side.
So, by using the above-stated property for the triangle ABP as:
$AB< AP+BP$
Now, by substituting the values of the AP and BP to get the maximum value of AB as:
$\begin{align}
  & AB< 65+60 \\
 & \Rightarrow AB< 125 \\
\end{align}$
So, it gives the condition that AB can have a value of less than $125.$
So, the largest value AB can have is $125-1=124$.
So, the largest value of side AB is $124.$
Hence, option (a) is correct.

Note: Now, to solve these types of the questions we need to know some of the basic properties of the triangle so that it will be easier for us to solve these types of problems. So, the properties required for these types of questions are: the sum of two sides of the triangle is always greater than the third side.
the condition of the similarity that the ratio of the sides of the similar triangles is always equal.