
ABCD is a quadrilateral. If
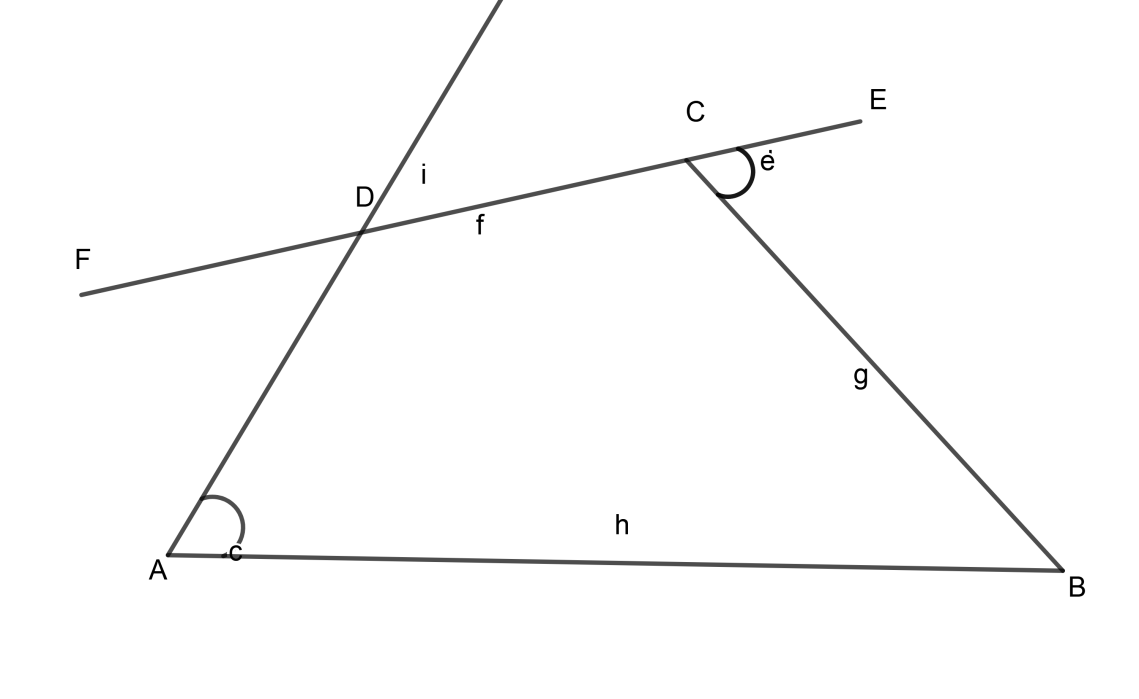

Answer
519k+ views
Hint: To prove the above statement use the property of cyclic quadrilateral i. e. opposite angles of a cyclic quadrilateral are always Supplementary i.e. their summation is
Complete step-by-step answer:
To prove that quadrilateral ABCD is a cyclic quadrilateral, we should know the necessary and sufficient condition for a quadrilateral to be cyclic which is given below,
Concept: Opposite angles of a cyclic quadrilateral are always Supplementary i.e. their summation is
Which means we have to prove,
Let,
From figure we can easily see that
But, from figure we can also write,
Therefore from above two equations we can write,
Put the value of equation (1),
Now we will add
By giving separate signs in bracket we can write,
Now, as we all know summation of all angles of a square is always
By rearranging above equation,
Put the value of Equation (3) in above equation,
From equations (3) and (4),
We can conclude that
Hence Proved.
Note:
1) The concept given by “opposite angles of a cyclic quadrilateral are always Supplementary” is very much essential to prove any quadrilateral as a cyclic quadrilateral.
2) I have inscribed above the quadrilateral in a circle geometrically therefore it is proved experimentally also. I have taken the mentioned angle as
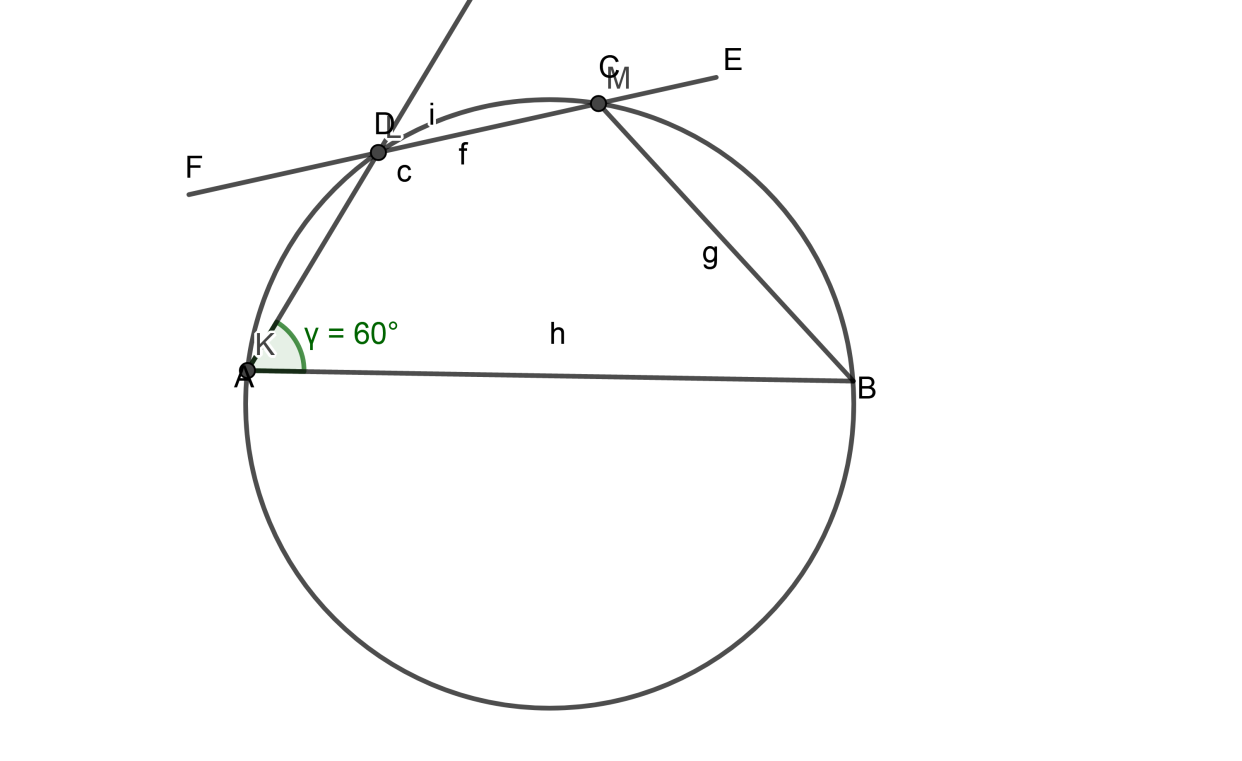
Complete step-by-step answer:
To prove that quadrilateral ABCD is a cyclic quadrilateral, we should know the necessary and sufficient condition for a quadrilateral to be cyclic which is given below,
Concept: Opposite angles of a cyclic quadrilateral are always Supplementary i.e. their summation is
Which means we have to prove,
Let,
From figure we can easily see that
But, from figure we can also write,
Therefore from above two equations we can write,
Put the value of equation (1),
Now we will add
By giving separate signs in bracket we can write,
Now, as we all know summation of all angles of a square is always
By rearranging above equation,
Put the value of Equation (3) in above equation,
From equations (3) and (4),
We can conclude that
Hence Proved.
Note:
1) The concept given by “opposite angles of a cyclic quadrilateral are always Supplementary” is very much essential to prove any quadrilateral as a cyclic quadrilateral.
2) I have inscribed above the quadrilateral in a circle geometrically therefore it is proved experimentally also. I have taken the mentioned angle as

Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Distinguish between the reserved forests and protected class 10 biology CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

Statistics in singular sense includes A Collection class 10 maths CBSE




