
ABCD is a quadrilateral in which all four sides are equal. Show that both pairs of opposite sides are equal.
Answer
501.6k+ views
Hint: Here, we will first draw quadrilateral ABCD with same sides length. Then we will draw AC and BC bisectors which will divide angles in equal parts. So, by this we will prove that
Complete step-by-step answer:
Here, if we assume that sides of quadrilateral ABCD are the same then interior angles will be also same with 90 degrees. So, we get figure as
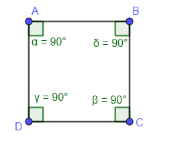
Thus, we can say that ABCD is square.
Now, if we draw diagonals AC and BD then, they will bisect interior angles and will meet at point O.
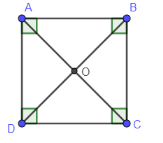
Now, we can say
So, we can say that
Now, since
By using alternate angle theorem which is given as two angles formed when a line crosses two other lines that lie on opposite sides of the transversal lines and opposite relative sides of the other lines.
We can say that
So, by converse theorem we can say that AB is parallel to CD. ……………..(1)
Similarly, if we take BD as bisector, we get angles to be equal as
Thus, we can say that
So, by converse theorem we can say that AD is parallel to BC. …………………..(2)
Hence, opposite sides are parallel quadrilateral ABCD are equal. Thus, proved.
Note: Students should know the concept of bisector. This is not to be proved by saying that as this quadrilateral is square then we know that the length of opposite sides is the same. We have to prove the interior angles are equal and then by converse theorem we have to give an answer. So, be careful while solving this type of problem.
Complete step-by-step answer:
Here, if we assume that sides of quadrilateral ABCD are the same then interior angles will be also same with 90 degrees. So, we get figure as

Thus, we can say that ABCD is square.
Now, if we draw diagonals AC and BD then, they will bisect interior angles and will meet at point O.

Now, we can say
So, we can say that
Now, since
By using alternate angle theorem which is given as two angles formed when a line crosses two other lines that lie on opposite sides of the transversal lines and opposite relative sides of the other lines.
We can say that
So, by converse theorem we can say that AB is parallel to CD. ……………..(1)
Similarly, if we take BD as bisector, we get angles to be equal as
Thus, we can say that
So, by converse theorem we can say that AD is parallel to BC. …………………..(2)
Hence, opposite sides are parallel quadrilateral ABCD are equal. Thus, proved.
Note: Students should know the concept of bisector. This is not to be proved by saying that as this quadrilateral is square then we know that the length of opposite sides is the same. We have to prove the interior angles are equal and then by converse theorem we have to give an answer. So, be careful while solving this type of problem.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




