Question

ABCD is a quadrilateral inscribed in a circle with center O, $\angle ADC=130{}^\circ $ and $AD=DC$. Calculate:

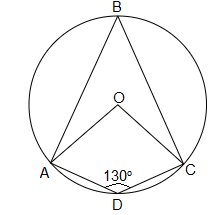
A) reflex $\angle AOC$
B) $\angle ABC$
C) $\angle AOD$

Answer 1

Hint: In part (i), use the theorem, the angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle’s circumference to find the value of the reflex $\angle AOC$. In part (ii), use the theorem, the sum of opposite angles of a cyclic quadrilateral is $180{}^\circ $ to find the value of \[\angle ABC\]. In part (iii), draw the line AD. After that, apply the kite property, the two angles are equal where the unequal sides meet which will give the value of $\angle OAD$. After that apply the isosceles triangle property to find the value of $\angle ODA$. Then apply the sum rule of the triangle to find the value of $\angle AOD$.

Complete step-by-step answer:
Given: - $\angle ADC=130{}^\circ $ and $AD=DC$
A) As we know that, the angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle’s circumference.
Then for the arc AC,
reflex $\angle AOC=2\angle ADC$
Substitute the value of $\angle ADC$ in the above equation,
reflex $\angle AOC=2\times 130{}^\circ $
Multiply the term on the right side,
reflex $\angle AOC=260{}^\circ $
Hence, the value of reflex $\angle AOC$ is $260{}^\circ $.

B) As we know that the sum of the opposite angles of a cyclic quadrilateral is $180{}^\circ $.
Then,
$\angle ABC+\angle ADC=180{}^\circ $
Substitute the value of $\angle ADC$ in the above equation,
$130{}^\circ +\angle ABC=180{}^\circ $
Move $130{}^\circ $ on the other side and subtract from $180{}^\circ $.
$\angle ABC=50{}^\circ $
Hence, the value of $\angle ABC$ is $50{}^\circ $.

C) Draw a line from O to D.

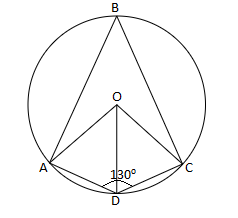
In quadrilateral AOCD,
$AD=DC$ (given)
$OA=OC$ (radius)
Then by kite property,
$\angle OAD=\angle OCD$
Also, the sum of the angles of a quadrilateral is equal to $360{}^\circ $.
$\angle OAD+\angle AOD+\angle OCD+\angle ACD=360{}^\circ $
Substitute the values,
$\angle OAD+100{}^\circ +\angle OAD+130{}^\circ =360{}^\circ $
Add the like terms,
$2\angle OAD+230{}^\circ =360{}^\circ $
Move $230{}^\circ $ to the other side and subtract from $360{}^\circ $.
$2\angle OAD=130{}^\circ $
Divide both sides by 2,
$\angle OAD=65{}^\circ $
Now in triangle OAD,
$OA=OD$ (radius)
As we know that the angles opposite to the equal sides of the triangles are equal.
$\angle OAD=\angle ODA$
Substitute the value of $\angle OAD$,
$\angle ODA=65{}^\circ $.
As we know that the sum of angles of a triangle is equal to $180{}^\circ $,
$\angle OAD+\angle ODA+\angle AOD=180{}^\circ $
Substitute the values,
$65{}^\circ +65{}^\circ +\angle AOD=180{}^\circ $
Add the terms on the left side,
\[130{}^\circ +\angle AOD=180{}^\circ \]
Move $130{}^\circ $ to the other side and subtract from $180{}^\circ $,
$\angle AOD=50{}^\circ $
Hence, the value of $\angle AOD$ is $50{}^\circ $.

Note: Part B can be done in another way.
Step by step answer: -
Given: - $\angle ADC=130{}^\circ $ and $AD=DC$
As we know that the sum of an angle and its reflex is $360{}^\circ $.
Then,
reflex $\angle AOC+\angle AOC=360{}^\circ $
Substitute the value of reflex $\angle AOC$ in the above equation,
$260{}^\circ +\angle AOC=360{}^\circ $
Move $260{}^\circ $ on the other side and subtract from $360{}^\circ $.
$\angle AOC=100{}^\circ $ ….. (1)
As we know that, the angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle’s circumference.
Then for the arc AC,
$\angle AOC=2\angle ABC$
Substitute the value of $\angle AOC$ from the equation (1),
$100{}^\circ =2\angle ABC$
Divide both sides by 2,
$\angle ABC=50{}^\circ $
Hence, the value of $\angle ABC$ is $50{}^\circ $.