Question

ABCD is a square of side \[2m\]. Charges of \[5nC, + 10nC\] and \[ - 5nC\] are placed at corners A, B and C respectively. What is the work done in transferring a charge of \[5\mu C\] from D to the point of intersection of the diagonals.

Answer 1

Hint: Here side of the square is given. By using side, firstly we will find the diagonal value. Then we will find the value of potential at point O and D due to all other three charges that are given in this particular question. Then we use the work done formula which is the product of charge and the potential difference (\[W = v.q\] ).


Complete step by step answer:
Given that, Side of Square ABCD\[ = 2m\]

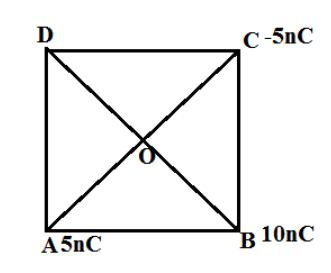
Three charges are given which are placed at the corner of the square (as shown).
Now we can see,
AC=BD=\[\sqrt {{{(2)}^2} + {{(2)}^2}} \] \[ = \sqrt {4 + 4} \]
=\[2\sqrt 2 \] \[ = 2.28m\]
Now, AO=BO=CO=\[\dfrac{{2.828}}{2} = 1.414m\]
Potential at O, \[{V_o} = \]\[\dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{{q_1}}}{{AO}} + \dfrac{{{q_2}}}{{BO}} + \dfrac{{{q_3}}}{{CO}}} \right]\]
Potential at D, \[{V_D} = \dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{{q_1}}}{{AD}} + \dfrac{{{q_2}}}{{BD}} + \dfrac{{{q_3}}}{{CD}}} \right]\]
Now, we know
Work done\[ = q\left[ {{v_O} - {v_D}} \right]\]
Charge \[q\] is given and we can find potential at point O and D .
So, W\[ = 5 \times {10^{ - 6}} \times 9 \times {10^9} \times \left[ {5 \times {{10}^{ - 9}}\left[ {\dfrac{1}{{AO}} - \dfrac{1}{{AD}}} \right] + 10 \times {{10}^{ - 9}}\left[ {\dfrac{1}{{BO}} - \dfrac{1}{{BD}}} \right]} \right]\]
\[\Rightarrow W = 45 \times {10^{ - 6}} \times {10^9} \times {10^{ - 9}}\left[ {5 \times \left( {\dfrac{1}{{1.414}} - \dfrac{1}{2}} \right) + 10 \times \left( {\dfrac{1}{{1.414}} - \dfrac{1}{{2.828}}} \right)} \right]\]
\[ \Rightarrow W = 450 \times {10^{ - 6}} \times \left( {\dfrac{1}{{1.414}} - \dfrac{1}{{2.828}}} \right)\]
\[\Rightarrow W = \dfrac{{450 \times {{10}^{ - 6}}}}{{1.414}}\left( {1 - \dfrac{1}{2}} \right) = 159.12 \times {10^{ - 6}}Joules\]
So, \[159.12 \times {10^{ - 6}}joules\] work is done transferring a charge of \[5\mu C\] from D to the point of intersection of diagonals.


Note: Potential difference between two points is the total amount of work is done to transfer a unit charge from one point to another. \[v = \dfrac{w}{q}\]
Here,\[v\] is the potential ,\[w\] is the work done and q is the charge. After knowing the value of potential and charge, we can easily find how much work is done. Work done is calculated in \[joules\] . When \[1 coulomb\] of charge is transferred and potential difference is \[1volt\] then the work done is said to be \[1joule.\]