Question

ABCDEF is a regular hexagon whose centre is O. Then $\overline{AB}+\overline{AC}+\overline{AD}+\overline{AE}+\overline{AF}$ is
(a) $2\overline{AO}$
(b) $3\overline{AO}$
(c) $5\overline{AO}$
(d) $6\overline{AO}$

Answer 1

Hint: First, we will construct the regular hexagon ABCDEF with center O. Then, we know from the study of the vectors we get \[\overline{AB}+\overline{BC}=\overline{AC}\]. Then, by using the similar conditions of the vectors for the other sides, we get more relations. Then, we got to know that $\overline{AB}$and $\overline{AC}$ are vectorially opposite to \[\overline{DE}\] and $\overline{DF}$.Then by using this condition, we get our final answer.

Complete step-by-step solution:
In this question, we are supposed to find the relational value of $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF}$in a regular hexagon.
So, firstly we will construct the regular hexagon ABCDEF with center O as:

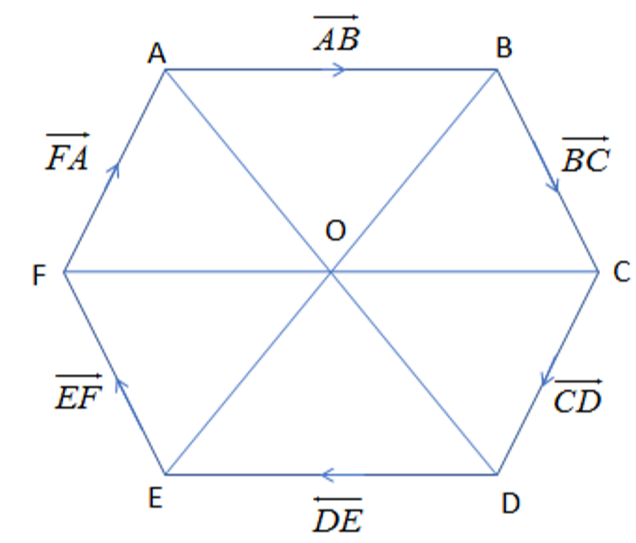
So, we know from the study of the vectors and the diagram as:

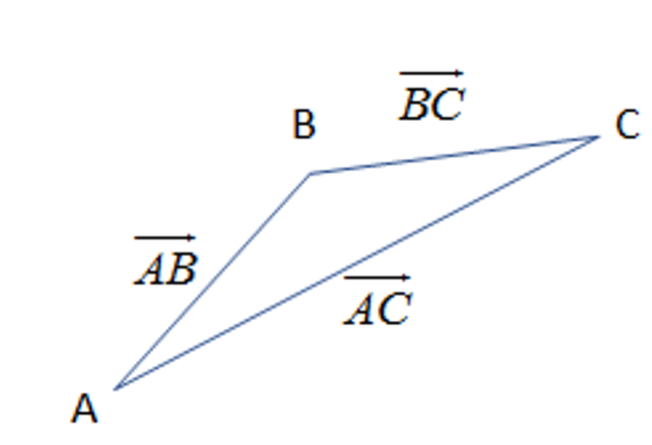
\[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]
So, by using the above relation, we get the following expression as:
\[\begin{align}
  & \overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AB}+\left( \overrightarrow{AB}+\overrightarrow{BC} \right) \\
 & \Rightarrow \overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AB}+\overrightarrow{BC}.....\left( i \right) \\
\end{align}\]
Now, similarly we can draw the downside of the figure which gives the following relation as:
\[\overrightarrow{AE}=\left( \overrightarrow{AD}+\overrightarrow{DE} \right).....\left( ii \right)\]
Now, again using the figure, we get the relation as:
\[\overrightarrow{AF}=\left( \overrightarrow{AD}+\overrightarrow{DE}+\overrightarrow{EF} \right).....\left( iii \right)\]
Now, from the figure, by applying the vector addition theorem, we get:
\[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AD}\].
Similarly, by using the vector addition again, we can do with the other side of the hexagon which gives us as \[\overrightarrow{AF}+\overrightarrow{FE}+\overrightarrow{ED}=\overrightarrow{AD}\].
So, by using the equations (i), (ii) and (iii), we get:
$\begin{align}
  & \overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF} \\
 & \Rightarrow 2\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AD}+\left( \overrightarrow{AD}+\overrightarrow{DE} \right)+\left( \overrightarrow{AD}+\overrightarrow{DE}+\overrightarrow{EF} \right) \\
\end{align}$
Now, by using the figure drawn which shows the vector starting and end point, we can conclude that $\overrightarrow{AB}$and $\overrightarrow{BC}$ are vectorially opposite to \[\overrightarrow{DE}\] and $\overrightarrow{EF}$.
So, we get the above expression by substituting the value of $\overrightarrow{AB}=-\overrightarrow{DE}$ and $\overrightarrow{BC}=-\overrightarrow{EF}$, we get:
$\begin{align}
  & -2\overrightarrow{DE}-\overrightarrow{EF}+\overrightarrow{AD}+\left( \overrightarrow{AD}+\overrightarrow{DE} \right)+\left( \overrightarrow{AD}+\overrightarrow{DE}+\overrightarrow{EF} \right) \\
 & \Rightarrow 3\overrightarrow{AD} \\
\end{align}$
So, we get the result from the above calculation as:
$\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF}=3\overrightarrow{AD}$
Then, from the figure, it is clear that:
$\overrightarrow{AD}=2\overrightarrow{AO}$
So, the above expression will give us the following result as:
\[\begin{align}
  & \overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF}=3\left( 2\overrightarrow{AO} \right) \\
 & \Rightarrow \overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF}=6\overrightarrow{AO} \\
\end{align}\]
So, the value of the expression \[\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF}\] is \[6\overrightarrow{AO}\].
Hence, option (d) is correct.

Note: To solve this type of problem, we must be aware of the use of the vectors as they can give us the desiring results to get the final answer. Like in this question, we need the relations between the sides of the regular hexagon ABCDEF with center O. Or So, by using the vector directions, we get the result as \[\overline{AB}+\overline{BC}=\overline{AC}\].

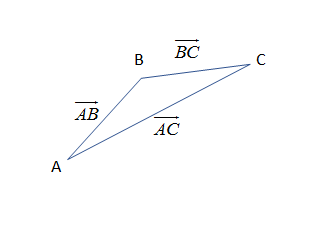
Similarly, it can be done with either side of the hexagon and the final result must be calculated accordingly.