Question

ABCH is a square with side $ 10 $ cm, while FCDE is another square with side $ 6 $ cm. AD is joined by intersecting HC at K. Find the area of trapezium FKDE.

Answer 1

Hint: Here we will redraw the figure and extend the figure to make it rectangle. Observe the given figure twice and start solving using the formula of rectangles. Find the correlation among the parts of the figure and find the required area.

Complete step-by-step answer:

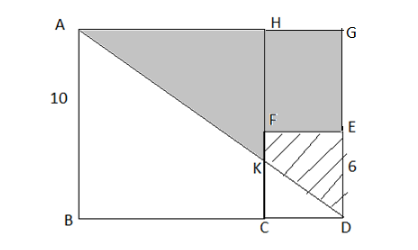
Redraw the figure as shown in the above figure.
Now, BD is $ = BC + CD $
Place values
 $
   \Rightarrow BD = 10 + 6 \\
   \Rightarrow BD = 16\;cm \;
  $
So, ABDG is the rectangle with the length of $ 16\;cm $ and the breadth of $ 10\;cm $
Therefore, the area of the rectangle is $ A = l \times b $
Place values –
 $ A = 16 \times 10 $
Simplify the equation –
 $ A = 160{\text{ c}}{{\text{m}}^2} $
Since, the diagonal divides the rectangle in two parts, the area of AGD will be half of the rectangle.
Area of AGD $ = \dfrac{{160}}{2} $
Area of AGD $ = 80\;c{m^2} $ .... (A)
Now, given that FCDE is the square with side $ 6 $ cm, so HG is also $ 6 $ cm and also
 $ HF + FC = AB $
Place known values
 $
  HF + 6 = 10 \\
  HF = 10 - 6 \\
  HF = 4\;cm \;
  $
Opposite side of HF, GE is also $ 4 $ cm.
So, EFHG is the rectangle with length $ 6cm $ and breadth $ 4cm $ .
Area of EFHG $ = l \times b $
Place values in the above equation –
Area of EFHG $ = 6 \times 4 $
Area of EFHG $ = 24\;c{m^2} $ ... (B)
Now, the area of FEDK is the area of AGD –Area of EFHG
 By using the values of equation (A) and (B)
Area of FEDK $ = 80 - 24 $
Simplify the above expression –
Area of FEDK $ = 56\;c{m^2} $
This is the required solution.
So, the correct answer is “ $ = 56\;c{m^2} $”.

Note: Always observe the given figure and find out the ways, as here we are asked to find the area of a very uneven figure. So, always try to convert the figure in the form of known formulas for the area as such we did in extending the figure and making the rectangle. Be careful while placing the values and its simplification.