

Answer
524.4k+ views
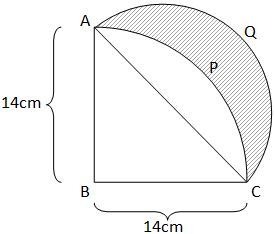
Hint: In this question, to find the area of shaded portion we have to calculate the area of region
Complete step-by-step answer:
In right angle triangle
Using Pythagoras theorem
Area of region
Now, area of shaded portion = Area of semicircle
Therefore, the area of shaded region is
Hence, the correct option is C.
Note: In order to solve such questions where the area under the shaded portion needs to be found out the basic step is to find out the geometrical figures around the shaded portion as sometimes the shaded portion might not be in some known geometrical form. So, we mostly find out the geometrical figures at the boundary of the region and subtract the area between them.
Complete step-by-step answer:
In right angle triangle
Using Pythagoras theorem
Area of region
Now, area of shaded portion = Area of semicircle
Therefore, the area of shaded region is
Hence, the correct option is C.
Note: In order to solve such questions where the area under the shaded portion needs to be found out the basic step is to find out the geometrical figures around the shaded portion as sometimes the shaded portion might not be in some known geometrical form. So, we mostly find out the geometrical figures at the boundary of the region and subtract the area between them.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Draw a diagram of a flower and name the parts class 12 biology ICSE




