Question

AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, AD bisects BC.

Answer 1

Hint: In this question, we are supposed to prove that AD bisects BC. This means, BD = DC. To solve this question, first of all we will draw the isosceles triangle ABC with AB = AC. Then we will apply Pythagoras theorem in the two triangles which will be formed (triangle ADB and triangle ADC). With the results of the Pythagoras Theorem, we will prove that BD = DC.

Complete step by step answer:
To begin with, let us draw an isosceles triangle ABC with sides AB = AC. Then we will draw a line segment perpendicular to side BC at point D and passing through vertex A. This will be the altitude of the triangle ABC.

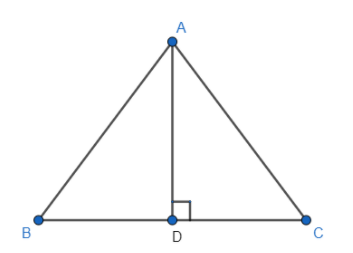
According to Pythagoras theorem, the sum of the squares of two sides adjacent to the right angle in a right-angled triangle is equal to the square of the side opposite to the right angle.
Now, in triangle ADB, we will apply Pythagoras Theorem.
$\Rightarrow A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}}......\left( 1 \right)$
Similarly, in triangle ADC, we will apply Pythagoras Theorem.
$\Rightarrow A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}}......\left( 2 \right)$
Since, triangle ABC is an isosceles triangle, AB = AC
$\Rightarrow A{{B}^{2}}=A{{C}^{2}}$
This implies that (1) = (2)
Therefore, $A{{D}^{2}}+B{{D}^{2}}=A{{D}^{2}}+D{{C}^{2}}$.
Now, $A{{D}^{2}}$ cancels out from LHS and RHS.
 $\Rightarrow B{{D}^{2}}=D{{C}^{2}}$
This means, BD = DC, since BD and DC are both lengths and neither of them can be negative.

Note: This solution is a standard solution that in an isosceles triangle, the altitude is the perpendicular bisector of the base of the given isosceles triangle. Students are advised to always draw figures in such types of questions as it helps understanding the conditions in a better way.