Question

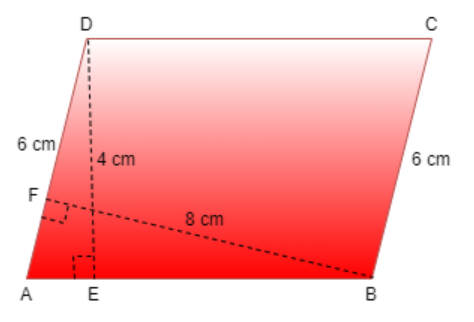
Altitude DE and BF of parallelogram ABCD are 4 cm and 8 cm respectively. One side AD is 6 cm long. Find the perimeter of parallelogram ABCD.

Answer 1

Hint: In this question remember to read the given information to identify the given dimensions and remember that area of a parallelogram is given as; base $ \times $ corresponding height, using this information will help you to approach the solution.

Complete step-by-step solution:
According to the given information we have DE = 4 cm, BF = 8 cm and AD = 6 cm
Using the formula of area of parallelogram i.e. base $ \times $ corresponding height
Now for parallelogram ABCD
Area of parallelogram ABCD taking AD as base = AD $ \times $ BF
Substituting the given values in the above equation we get
Area of parallelogram ABCD with base AD = 6 $ \times $ 8
Area of parallelogram ABCD with base AD = 48 $c{m^2}$
Now area of parallelogram ABCD taking base AB = AB $ \times $ DE
Substituting the given values in the above equation we get
Area of parallelogram ABCD with base AB = AB $ \times $ 4
Since we know that area of parallelogram ABCD with base AD = area of parallelogram ABCD with base AB
So, 48 = AB $ \times $ 4
$ \Rightarrow $ AB = $\dfrac{{48}}{4}$
$AB = 12 cm$
Now using the formula of perimeter of parallelogram ABCD = 2 (base length + side length)
So, perimeter of parallelogram $ABCD = 2 (AB + AD) $
Substituting the given values in the above formula we get
Perimeter of the parallelogram $ABCD = 2 (12 + 6) $
Perimeter of the parallelogram ABCD = 2 $ \times $ 18 = 36 cm
So, the perimeter of the parallelogram ABCD is 36 cm.

Note: In the above solution the term parallelogram which can be defined as the shape which is a quadrilateral with sides opposite and parallel to each other due to which opposite angles are also equal to each other. The parallelogram which consists of all right angles is called a rectangle and the parallelogram whose all sides are equal to each other is called a rhombus.