
An equilateral triangle, a square and a circle have equal parameters. If T denotes the area of the triangle, S is the area of the square and C is the area of the circle, then:
A.
B.
C.
D.
Answer
430.5k+ views
Hint: For solving this question you should know about the areas of a triangle, square and a circle. IN this problem we will first find the areas of triangle, square and circle and then we will compare all the areas with each other.
Complete step-by-step solution:
According to the question, it is asked that an equilateral triangle, a square and a circle have equal parameters. And if T denotes the area of the triangle, S is the area of the square and C is the area of the circle. If we consider that the perimeters of each figure to be
The sides of the equilateral triangle will be
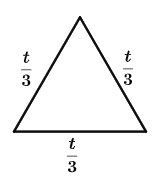
And the sides of the square will be
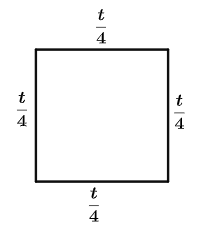
And the radius of the circle will be
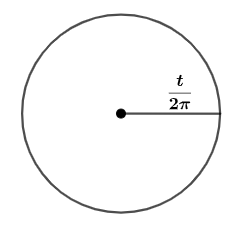
Since we know that the area of an equilateral triangle is equal to
As we know that the area of a square is
And we know that the area of the circle is
So, all the areas are:
So, the correct option is C.
Note: While solving this question you should know about the areas of the given shapes. And if in any question the parameters are given then we have to calculate the areas according to the measurements. And by using these we can also calculate the parameters of each other if any one is common from their area or peripherance.
Complete step-by-step solution:
According to the question, it is asked that an equilateral triangle, a square and a circle have equal parameters. And if T denotes the area of the triangle, S is the area of the square and C is the area of the circle. If we consider that the perimeters of each figure to be
The sides of the equilateral triangle will be

And the sides of the square will be

And the radius of the circle will be

Since we know that the area of an equilateral triangle is equal to
As we know that the area of a square is
And we know that the area of the circle is
So, all the areas are:
So, the correct option is C.
Note: While solving this question you should know about the areas of the given shapes. And if in any question the parameters are given then we have to calculate the areas according to the measurements. And by using these we can also calculate the parameters of each other if any one is common from their area or peripherance.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




