Question

An equilateral triangle of side 9 cm inscribed in a circle. The radius of the circle is
(a) 3 cm
(b) $ \sqrt{3} $ cm
(c) $ 3\sqrt{3} $ cm
(d) $ \dfrac{3\sqrt{3}}{2} $ cm

Answer 1

Hint: First, before proceeding for this, we must draw the circle with triangle ABC at centre O and has perpendicular OD on side BC of the equilateral triangle ABC so that we can easily analyse the question. Then, by using the rules of the congruency of the triangles, we can get $ \Delta OBD $ and $ \Delta ODC $ as congruent. Then, by using another property of the triangle circumscribed in the circle is that the angle subtended by an arc at the centre is double the angle subtended by it at any point in the remaining part of the circle. Then, by applying the trigonometric identity in the triangle BOD, we get the desired value of radius.

Complete step-by-step answer:
In this question, we are supposed to find the radius of the circle when that circle inscribes an equilateral triangle with side 9 cm.
So, before proceeding for this, we must draw the circle with triangle ABC at centre O and has perpendicular OD on side BC of the equilateral triangle ABC so that we can easily analyse the question as:

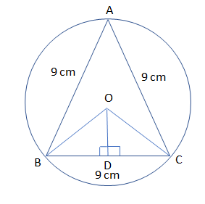
Now, first thing we have is that triangle ABC is an equilateral triangle which gives:
AB=BC=CA=9 cm
Then, we can see from the diagram that O is the circumcentre of triangle ABC and OD is perpendicular on the side BC which cuts BC in two equal halves.
Now, by using the rules of the congruency of the triangles, we can get $ \Delta OBD $ and $ \Delta ODC $ as congruent.
So, by using the conditions as:
OB=OC (Radius of the circle)
BD=DC (D is the mid point of BC)
OD=OD (common)
So, by using the SSS(side-side-side) congruency, we get the above condition fulfilled that $ \Delta OBD $ is congruent to $ \Delta ODC $ .
So, when we get these two triangles as congruent then other angles and side are also equal.
The, we also get a condition that:
 $ \angle BOD=\angle COD $
Now, by using another property of the triangle circumscribed in the circle is that the angle subtended by an arc at the centre is double the angle subtended by it at any point in the remaining part of the circle.
So, this condition provides us with the equation as:
 $ \angle BOC=2\angle BAC $
Now, we also know that an equilateral triangle has all of its angles equal to $ {{60}^{\circ }} $ which gives $ \angle BAC={{60}^{\circ }} $ .
Now, we get the value of above expression as:
 $ \begin{align}
  & \angle BOC=2\times {{60}^{\circ }} \\
 & \Rightarrow \angle BOC={{120}^{\circ }} \\
\end{align} $
Now, we can see clearly from the figure that:
 $ \begin{align}
  & \angle BOD=\dfrac{\angle BOC}{2} \\
 & \Rightarrow \angle BOD=\dfrac{{{120}^{\circ }}}{2} \\
 & \Rightarrow \angle BOD={{60}^{\circ }} \\
\end{align} $
Moreover, we also get:
 $ \begin{align}
  & BD=\dfrac{BC}{2} \\
 & \Rightarrow BD=\dfrac{9}{2} \\
\end{align} $
Now, by applying the trigonometric identity in the triangle BOD, we get:
 $ \sin \angle BOD=\dfrac{BD}{OB} $
Then, by substituting all the values, we get:
 $ \begin{align}
  & \sin {{60}^{\circ }}=\dfrac{\dfrac{9}{2}}{OB} \\
 & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{\dfrac{9}{2}}{OB} \\
 & \Rightarrow OB=\dfrac{9}{2}\times \dfrac{2}{\sqrt{3}} \\
 & \Rightarrow OB=3\sqrt{3} \\
\end{align} $
So, we get the value of radius as $ 3\sqrt{3} $ cm.
So, the correct answer is “Option C”.

Note: Now, to solve these types of questions we need to know some of the basic trigonometric rules for the right angled triangle with base b, perpendicular p and hypotenuse h. So the conditions to be kept in mind are:
 $ \begin{align}
  & \tan \theta =\dfrac{p}{b} \\
 & \sin \theta =\dfrac{p}{h} \\
 & \cos \theta =\dfrac{b}{h} \\
\end{align} $