
An exterior angle of a triangle is $100^\circ $ and its interior opposite angles are equal to each other. Find the measure of each angle of the triangle.
Answer
553.8k+ views
Hint:
We will take the unknown measures as $x^\circ $. Then we will equate the sum of interior angles to the exterior angle and find the unknown interior angles. Finally, we will use the angle sum property of a triangle to find the third angle.
Complete step by step solution:
Let us consider $\vartriangle ABC$. Let us assume that the exterior angle is formed by producing the side $BC$ along the line $CD$.
We are given that the exterior angle is $100^\circ $. Let us take $\angle ACD = 100^\circ $.
Also, it is given that the interior opposite angles are equal. Let us take each of them to be $x^\circ $i.e., $\angle BAC = \angle ABC = x^\circ $.
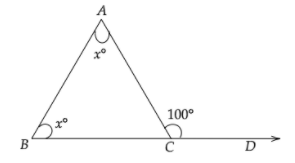
We know that “If the side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles”.
Applying this to $\vartriangle ABC$, we get
$\angle BAC + \angle ABC = 100^\circ $……………………..$\left( 1 \right)$
Substituting $\angle BAC = \angle ABC = x^\circ $ in equation $\left( 1 \right)$, we get
$ \Rightarrow x^\circ + x^\circ = 100^\circ $
Adding the like terms on the LHS, we get
$ \Rightarrow 2x^\circ = 100^\circ $
Dividing both sides by 2, we get
$ \Rightarrow x^\circ = \dfrac{{100^\circ }}{2} = 50^\circ $
Therefore, $\angle BAC = \angle ABC = 50^\circ $. Now, we will use the angle sum property of a triangle to find the third angle. We know that “Sum of the angles of a triangle is $180^\circ $”.
Applying this to $\vartriangle ABC$,
$\angle ABC + \angle BAC + \angle ACB = 180^\circ $ ……………………………………$\left( 2 \right)$
Substituting $\angle BAC = \angle ABC = 50^\circ $ in equation $\left( 2 \right)$, we get,
$ \Rightarrow 50^\circ + 50^\circ + \angle ACB = 180^\circ $
Adding the like terms, we get
$ \Rightarrow 100^\circ + \angle ACB = 180^\circ $
Subtracting $100^\circ $ on both the sides, we get
$ \Rightarrow \angle ACB = 180^\circ - 100^\circ = 80^\circ $
Thus, the angles of $\vartriangle ABC$ are $50^\circ ,50^\circ {\text{ and }}100^\circ $.
Note:
We can also find $\angle ACB$ as follows:
Since $BD$ is a line, $\angle ACB{\text{ and }}\angle ACD$ form a linear pair.
Now, we know that the sum of a linear pair of angles is $180^\circ $. Therefore,
$\angle ACB + \angle ACD = 180^\circ $
Substituting $\angle ACD = 100^\circ $ in the above equation, we get
$\angle ACB = 180^\circ - 100^\circ = 80^\circ $
Now again using angle sum property, we get
$\angle ABC + \angle BAC + \angle ACB = 180^\circ $
Substituting the values in the above equation, we get
$ \Rightarrow x + x + 80^\circ = 180^\circ $
Adding and subtracting the like terms, we get
$\Rightarrow 2x = 180^\circ - 80^\circ \\
\Rightarrow 2x = 100^\circ \\ $
Dividing both side by 2, we get
$ \Rightarrow x = 50^\circ $
Thus, the angles of $\vartriangle ABC$ are $50^\circ ,50^\circ {\text{ and }}100^\circ $.
We will take the unknown measures as $x^\circ $. Then we will equate the sum of interior angles to the exterior angle and find the unknown interior angles. Finally, we will use the angle sum property of a triangle to find the third angle.
Complete step by step solution:
Let us consider $\vartriangle ABC$. Let us assume that the exterior angle is formed by producing the side $BC$ along the line $CD$.
We are given that the exterior angle is $100^\circ $. Let us take $\angle ACD = 100^\circ $.
Also, it is given that the interior opposite angles are equal. Let us take each of them to be $x^\circ $i.e., $\angle BAC = \angle ABC = x^\circ $.

We know that “If the side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles”.
Applying this to $\vartriangle ABC$, we get
$\angle BAC + \angle ABC = 100^\circ $……………………..$\left( 1 \right)$
Substituting $\angle BAC = \angle ABC = x^\circ $ in equation $\left( 1 \right)$, we get
$ \Rightarrow x^\circ + x^\circ = 100^\circ $
Adding the like terms on the LHS, we get
$ \Rightarrow 2x^\circ = 100^\circ $
Dividing both sides by 2, we get
$ \Rightarrow x^\circ = \dfrac{{100^\circ }}{2} = 50^\circ $
Therefore, $\angle BAC = \angle ABC = 50^\circ $. Now, we will use the angle sum property of a triangle to find the third angle. We know that “Sum of the angles of a triangle is $180^\circ $”.
Applying this to $\vartriangle ABC$,
$\angle ABC + \angle BAC + \angle ACB = 180^\circ $ ……………………………………$\left( 2 \right)$
Substituting $\angle BAC = \angle ABC = 50^\circ $ in equation $\left( 2 \right)$, we get,
$ \Rightarrow 50^\circ + 50^\circ + \angle ACB = 180^\circ $
Adding the like terms, we get
$ \Rightarrow 100^\circ + \angle ACB = 180^\circ $
Subtracting $100^\circ $ on both the sides, we get
$ \Rightarrow \angle ACB = 180^\circ - 100^\circ = 80^\circ $
Thus, the angles of $\vartriangle ABC$ are $50^\circ ,50^\circ {\text{ and }}100^\circ $.
Note:
We can also find $\angle ACB$ as follows:
Since $BD$ is a line, $\angle ACB{\text{ and }}\angle ACD$ form a linear pair.
Now, we know that the sum of a linear pair of angles is $180^\circ $. Therefore,
$\angle ACB + \angle ACD = 180^\circ $
Substituting $\angle ACD = 100^\circ $ in the above equation, we get
$\angle ACB = 180^\circ - 100^\circ = 80^\circ $
Now again using angle sum property, we get
$\angle ABC + \angle BAC + \angle ACB = 180^\circ $
Substituting the values in the above equation, we get
$ \Rightarrow x + x + 80^\circ = 180^\circ $
Adding and subtracting the like terms, we get
$\Rightarrow 2x = 180^\circ - 80^\circ \\
\Rightarrow 2x = 100^\circ \\ $
Dividing both side by 2, we get
$ \Rightarrow x = 50^\circ $
Thus, the angles of $\vartriangle ABC$ are $50^\circ ,50^\circ {\text{ and }}100^\circ $.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who among the following opened first school for girls class 9 social science CBSE

What does the word meridian mean A New day B Midday class 9 social science CBSE

What is the full form of pH?

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it




