Question

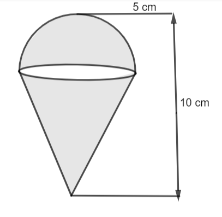
An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown. Calculate the volume of the ice cream (to the nearest integer, in \[c{{m}^{3}}\]), provided that its \[\dfrac{1}{6}th\] part is left unfilled with ice cream. Insert the answer in the nearest integer.

Answer 1

Hint: To solve the above question, we will assume that the total volume of the ice cream will be equal to the sum of the volume of the upper hemisphere and the volume of the cone. So first we will find their individual volumes by applying their formula. We will first find out the actual height of the cone before calculating its volume. Also, we will assume that the radius of the hemisphere is equal to the radius of the cone.

Complete step-by-step answer:
We have to find the volume of the ice cream. The total volume of the ice cream will be the sum of the volume of the upper hemisphere and the volume of the cone. Now, we are given the total height of the ice cream cone as 10 cm. The total height of the ice cream cone is the sum of the radius of the hemisphere and the height of the cone. Thus we have
Radius + Height = 10 cm
\[\Rightarrow 5cm+\text{ height }=10cm\]
\[\Rightarrow \text{height }=10cm\]
Now, we will calculate the individual volumes of the cone and hemisphere. The volume of the cone with height h and radius r is given by the formula
\[\text{Volume of the cone}=\dfrac{1}{3}\pi {{r}^{2}}h\]
In our case, r = radius of the hemisphere = 5 cm and height = 5 cm. Thus,
\[\text{Volume of the cone}=\dfrac{1}{3}\pi {{\left( 5cm \right)}^{2}}\times 5cm\]
\[\Rightarrow \text{Volume of the cone}=\dfrac{1}{3}\times \pi \times 125c{{m}^{3}}\]
\[\Rightarrow \text{Volume of the cone}=\dfrac{125\pi }{3}c{{m}^{3}}\]
The volume of the hemisphere is given by the following formula
\[\text{Volume of the hemisphere}=\dfrac{2}{3}\pi {{r}^{3}}\]
where r is the radius of the hemisphere. In our case, r = 5cm. Thus,
\[\text{Volume of the hemisphere}=\dfrac{2}{3}\times \pi \times {{\left( 5cm \right)}^{3}}\]
\[\Rightarrow \text{Volume of the hemisphere}=\dfrac{2}{3}\times \pi \times 125c{{m}^{3}}\]
\[\Rightarrow \text{Volume of the hemisphere}=\dfrac{250\pi }{3}c{{m}^{3}}\]
Now, the total volume of the ice cream is the sum of the volumes of the cone and hemisphere. Thus, we will get,
Total Volume = Volume of the cone + Volume of the hemisphere
\[\Rightarrow \text{Total Volume}=\dfrac{125\pi }{3}c{{m}^{3}}+\dfrac{250}{3}c{{m}^{3}}\]
\[\Rightarrow \text{Total Volume}=\dfrac{375\pi }{3}c{{m}^{3}}\]
\[\Rightarrow \text{Total Volume}=125\pi c{{m}^{3}}\]
Now, it is given in the question that \[\dfrac{1}{6}th\] of the total is left unfilled. Thus, the required volume will be
\[\text{Required volume}=\text{ Total volume }-\dfrac{1}{6}\text{ of the total volume}\]
\[\Rightarrow \text{Required volume}=125\pi c{{m}^{3}}\left( 1-\dfrac{1}{6} \right)\]
\[\Rightarrow \text{Required volume}=125\pi c{{m}^{3}}\times \dfrac{5}{6}\]
\[\Rightarrow \text{Required volume}=125\times \dfrac{22}{7}\times \dfrac{5}{6}c{{m}^{3}}\]
\[\Rightarrow \text{Required volume}=327.38c{{m}^{3}}\]
\[\Rightarrow \text{Required volume }\left( \text{to the nearest integer} \right)=327c{{m}^{3}}\]

Note: While solving the question, we assumed that the cone is the right circular cone. This means the apex of the cone is right above the center of the circular base. That’s why we have applied the formula of the volume of the right circular cone. We can’t find its volume if the cone is not right circular in this case.