Question

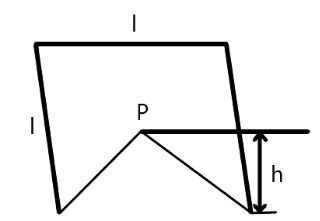
An isosceles triangle is to be cut from one edge of a square lamina (as shown in the figure) such that the remaining position when suspended from the apex $P$ of the cut will remain in equilibrium in any position. The value of $h$ is

A. $\dfrac{{\left( {3 - \sqrt 3 } \right)l}}{2}$
B. $\dfrac{{\left( {3 + \sqrt 3 } \right)l}}{2}$
C. $\dfrac{{\left( {2 - \sqrt 2 } \right)l}}{2}$
D. $\dfrac{{\left( {2 + \sqrt 2 } \right)l}}{2}$

Answer 1

Hint: Here, a square is given from which an isosceles triangle is to be cut. Therefore, we have an isosceles triangle and square. Therefore, we will use the formula for the area of the triangle for the isosceles triangle and the area of the lamina for the square.

Formula used:
The formula of the area of triangle is given by
${A_t} = \dfrac{1}{2}hl$
Here, $l$ is the length of the square from the triangle is to be cut down and $h$ is the height of the triangle.
The formula of the area of lamina is given below
${A_l} = {l^2} - {A_t}$
Here, $l$ is the length of the square and ${A_t}$ is the area of the triangle.

Complete step by step answer:
Here, an isosceles triangle is cut down from the square. Therefore, the area of triangle is given below
${A_t} = \dfrac{1}{2}hl$
Also, the area of lamina is given below
${A_l} = {l^2} - {A_t}$
Now, putting the value of area of triangle in the above formula as shown below
${A_l} = {l^2} - \dfrac{1}{2}hl$
$ \Rightarrow \,{A_l} = l\left( {l - \dfrac{1}{2}h} \right)$
Now, the center of mass of the triangle will be situated on its altitude at distance $\dfrac{h}{3}$ from the base. Now, according to the question, the center of mas of lamina is situated at P.
Now, according the diagram, the center of mass of the square is at point C, therefore, we get the following relation
${A_t}\left( {\dfrac{l}{2} - \dfrac{h}{3}} \right) = {A_l}\left( {\dfrac{l}{2} - \left( {l - h} \right)} \right)$
$ \Rightarrow \,\dfrac{1}{2}hl\left( {\dfrac{l}{2} - \dfrac{h}{3}} \right) = l\left( {l - \dfrac{1}{2}h} \right) \times \left( {\dfrac{l}{2} - \left( {l - h} \right)} \right)$
$ \Rightarrow \,\dfrac{2}{3}{h^2} - 2hl + {l^2} = 0$
$ \Rightarrow \,2{h^2} - 6hl + 2{l^2} = 0$
Now, we will use the quadratic formula to solve the above equation as shown below
$h = \dfrac{{6l \pm \sqrt {{{\left( {6l} \right)}^2} - 4 \times 2 \times 2{l^2}} }}{{2 \times 2}}$
$ \Rightarrow \,h = \dfrac{{6l \pm \sqrt {36{l^2} - 16{l^2}} }}{4}$
$ \Rightarrow \,h = \dfrac{{6l \pm \sqrt {20{l^2}} }}{4}$
$ \Rightarrow h = \dfrac{{6l \pm 2l\sqrt 3 }}{4}$
$ \therefore \,h = \left( {\dfrac{{3 \pm \sqrt 3 }}{2}} \right)l$
Now, the root $\left( {\dfrac{{3 - \sqrt 3 }}{2}} \right)l$ satisfies the condition $0 < h < l$. Therefore, the value of $h$ is $\left( {\dfrac{{3 - \sqrt 3 }}{2}} \right)l$.

Hence, option (A) is correct.

Note: We have used the formula of lamina because the square here behaves like a sheet from which an isosceles triangle is taken out. Here, we have used the quadratic formula because we cannot make factors of the equation. Also, the quadratic formula is used to find the value of $h$ which is in the form of $l$.