
An umbrella is made by stitching 12 triangular pieces of cloth. Each piece measures 50cm, 20cm and 50cm, find the area of the cloth used in it.
A.
B.
C.
D.

Answer
498.3k+ views
Hint: Given that umbrella is made of 12 triangular pieces of cloth. The area of the triangle when three sides are given is
Complete step-by-step answer:
We are given that an umbrella is made by stitching 12 triangular pieces of cloth and each piece measures 50cm, 20cm and 50cm.
We have to calculate the total area of cloth used to make the umbrella.
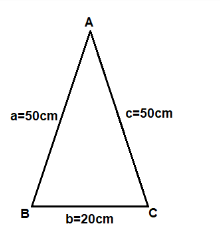
Area of one triangular piece is
Area of triangular piece is
Total area of the cloth used is
Therefore, the correct option is Option A,
So, the correct answer is “Option A”.
Note: Another approach
Area of the triangle =
So, height is not given in the question which means we have to find the height of the triangle using the given three sides’ measurements.
The given triangle is an isosceles triangle so the height will divide it into two smaller congruent triangles and the base will also be bisected.
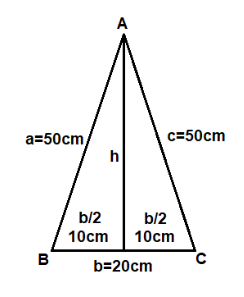
As we can see the diagram, the height divided the triangle into two right triangles.
Using Pythagoras theorem, we can find the height.
According to Pythagoras theorem, the hypotenuse square is equal to the sum of squares of the other two adjacent sides.
Area is
Total area of the cloth used is
Complete step-by-step answer:
We are given that an umbrella is made by stitching 12 triangular pieces of cloth and each piece measures 50cm, 20cm and 50cm.
We have to calculate the total area of cloth used to make the umbrella.

Area of one triangular piece is
Area of triangular piece is
Total area of the cloth used is
Therefore, the correct option is Option A,
So, the correct answer is “Option A”.
Note: Another approach
Area of the triangle =
So, height is not given in the question which means we have to find the height of the triangle using the given three sides’ measurements.
The given triangle is an isosceles triangle so the height will divide it into two smaller congruent triangles and the base will also be bisected.

As we can see the diagram, the height divided the triangle into two right triangles.
Using Pythagoras theorem, we can find the height.
According to Pythagoras theorem, the hypotenuse square is equal to the sum of squares of the other two adjacent sides.
Area is
Total area of the cloth used is
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Differentiate between the Western and the Eastern class 9 social science CBSE




