Question

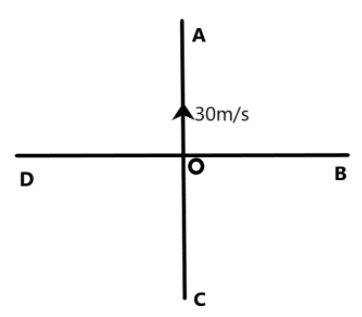
As shown in the figure, a source O of frequency 300Hz moves towards north with a velocity of 30\[m{{s}^{-1}}\]. A, B, C and D are four observers, each at a distance of 300m from O. Velocity of sound is 330\[m{{s}^{-1}}\]. As the source starts moving in the direction shown at \[t=0\] the frequency observed by A, B, C, and D will be (in Hz) –
                

A) Equal
B) 330, 300, 330, 300
C) 330, 330, 275, 250
D) 330, 300, 275, 300

Answer 1

Hint: We need to determine the variation of frequency with respect to the observers in a system. We know that the Doppler’s effect deals with the frequency variation in sound waves due to the relative velocity between the source and the listener.

Complete answer:
The Doppler’s effect for longitudinal waves such as sound deals with the fact that relative velocities between the source and the listener, in case of sound, can cause the listener to experience a change in the frequency of the sound from the source. According to Doppler effect,
\[{{f}_{new}}=f\dfrac{v+{{v}_{listener}}}{v+{{v}_{source}}}\]
Where, v is the speed of sound in the medium and f is the actual frequency of the source.
In our situation, we are given that there are four listeners for a single source of sound which is moving in a particular direction with a relative velocity to each of them. The relative velocities will result in different results for the different listeners.

Let us consider each of the listeners at the time, \[t=0\].
The Source O is moving towards the listener A with a velocity 30\[m{{s}^{-1}}\]. The source is approaching the stationary listener. The frequency as heard by A is given as –
\[\begin{align}
  & {{f}_{A}}=f\dfrac{v+{{v}_{A}}}{v+{{v}_{O}}} \\
 & \text{but,} \\
 & {{v}_{A}}=0,{{v}_{O}}=-30m{{s}^{-1}},f=300Hz,v=330m{{s}^{-1}} \\
 & \Rightarrow {{f}_{A}}=300\dfrac{330+0}{330-30} \\
 & \therefore {{f}_{A}}=330Hz \\
\end{align}\]
Similarly, we can find the frequency at C as follows –
\[\begin{align}
  & {{f}_{C}}=f\dfrac{v+{{v}_{C}}}{v+{{v}_{O}}} \\
 & \text{but,} \\
 & {{v}_{C}}=0,{{v}_{O}}=+30m{{s}^{-1}},f=300Hz,v=330m{{s}^{-1}} \\
 & \Rightarrow {{f}_{C}}=300\dfrac{330+0}{330+30} \\
 & \therefore {{f}_{C}}=275Hz \\
\end{align}\]
Now, we can consider the points B and D, these points do not have a longitudinal relation with the sound source. The sound source is moving perpendicular to their direction. Therefore, there experiences no change in the frequency by the listeners at B and D. So,
\[\begin{align}
  & {{f}_{B}}=f\dfrac{v+{{v}_{B}}}{v+{{v}_{O}}} \\
 & \text{but,} \\
 & {{v}_{B}}=0,{{v}_{O}}=0,f=300Hz,v=330m{{s}^{-1}} \\
 & \Rightarrow {{f}_{B}}={{f}_{D}}=300\dfrac{330+0}{330+0} \\
 & \therefore {{f}_{B}}={{f}_{D}}=300Hz \\
\end{align}\]
The frequencies heard by A, B, C and D are 330Hz, 300Hz, 275Hz and 300Hz respectively.

The correct answer is option D.

Note:
The longitudinal waves do not experience a Doppler’s change when the propagation of the wave is in direction perpendicular to the listener. Other waves such as the light waves experience Doppler’s effect along perpendicular direction also.