Question

Asymptote in a logistic growth curve is obtained when.
(A) ${ K }<{ N } $
(B) The value of 'r' approaches zero
(C) ${ K }={ N } $
(D) ${ K }>{ N } $

Answer 1

Hint: Asymptote in the logistic growth curve is obtained when carrying capacity is equal to the number of people during a population. A straight line that continually approaches a specific curve but does not meet it at any finite point is known as an asymptote.

Complete step by step answer:
- Asymptote in a logistic growth curve is obtained in a situation when ‘K = N’. When carrying capacity is equal to the number of individuals in the population, the line of the graph will be constant until there is an increase in population or there is a decrease in resources due to some reason.
- The population is a group of individuals having similar characteristic features.
- The size of the increase or decrease depending upon the time along with the environmental factors and other factors.

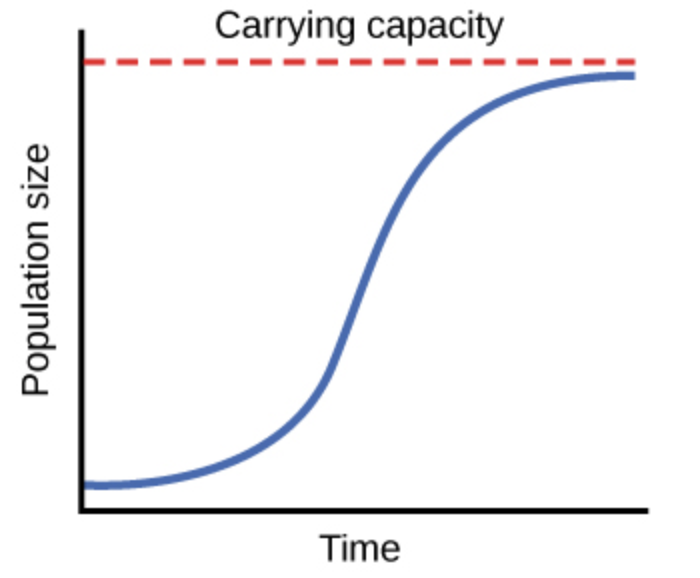
So, the correct answer is ‘${ K }={ N } $'.

Additional Information:
 A group of individuals of a similar species living within the same area is named a population. The measurement of how the dimensions of a population change over time is named the increase rate, and it depends upon the population size, birth rate, and death rate. As long as there are enough resources available, there'll be a rise in the number of people during the population overtime or a positive rate of growth. However, most populations cannot still grow forever because they're going to eventually run out of the water, food, sunlight, space, or other resources. As these resources begin to run out, the increase will start to hamper. When the expansion rate of a population decreases because the number of people increases, this is often called logistic increase. We can also check out logistic growth as a mathematical equation. An increased rate is measured in the number of people during a population (N) over time (t). The term for increase rate is written as $\frac { dN }{ dt } $.The d just means change. K represents the carrying capacity, and ‘r’ is the maximum per capita rate of growth for a population. Per capita means per individual, and therefore the per capita rate of growth involves the number of births and deaths during a population.
Logistic growth equation is $\frac { dN }{ dt } ={ rN }\left( \frac { K-N }{ K } \right) $
Note: As every equation in science has some assumption, the logistic growth curve also has some assumption and the assumption is that the K and r don't change over time in a population.