Question

At the top of the trajectory of a projectile, thrown at an angle of projection $\theta < {90^0}$, its
$\left( A \right)$ Velocity is zero.
$\left( B \right)$ Velocity is parallel to the direction of acceleration.
$\left( C \right)$ Velocity is anti-parallel to the direction of acceleration.
$\left( D \right)$ Velocity is perpendicular to the direction of acceleration.

Answer 1

Hint: In this question use the concept that projectile motion always follow the parabolic path and this parabola is opening vertically downward so it reaches a maximum point at some time of extent and at this time velocity is zero later on in the solution use the property that velocity is always tangential to the path of the projectile motion so use these concepts to reach the solution of the question.

Complete step-by-step solution -

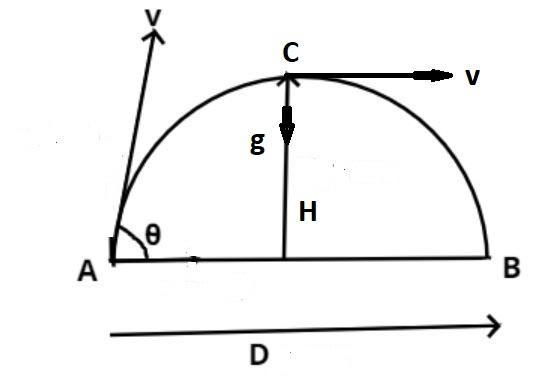
Consider the projectile motion as shown above in the figure let the particle be thrown from the point A with an angle $\theta < {90^0}$.
Doing so the particle reaches at maximum point C as shown in the figure and comes backs to ground at point B.
So once the particle reaches a maximum point the particle cannot go further high so the particle comes back from this point as shown above.
So at the highest point of the trajectory the velocity becomes zero, if not the particle goes further high which is only possible if velocity not becomes zero.
But at the highest point of the trajectory of a projectile the particle cannot go further high so the velocity of the particle becomes zero (as at this point acceleration due to gravity is equal to the earth gravity which makes the particle come down).
So this is the required answer.
So option (A) is the correct answer.

Now as we know that the direction of velocity is always tangent to the path as shown in the figure.
So at the highest point of trajectory during a projectile motion the velocity is again tangent to the path as shown in the figure.
But at the highest point of the trajectory the acceleration working on the particle is equal to the acceleration due to gravity (g) which is acting downward i.e. perpendicular to the tangential velocity.
So we can say that velocity is perpendicular to the direction of the acceleration.

So option (D) is also the correct answer.

Hence option (A) and (D) are the correct answer.

Note – Whenever we face such types of questions always recall that when a particle is thrown upwards, after reaching the maximum point the velocity of the particle becomes zero and the particle cannot go further high (as at this point acceleration due to gravity is equal to the earth gravity which makes the particle come down).